检索
E-mail
RSS

作者投稿 主编审稿 专家审稿 远程编辑

热带海洋学报 >

2017 , Vol. 36 >Issue 3: 46 - 54

DOI: https://doi.org/10.11978/2016079

大亚湾的潮汐动力学研究——Ⅱ.潮位和潮流双峰现象的产生机制

  • 严聿晗 , 1, 2 ,
  • 武文 2 ,
  • 宋德海 , 1 ,
  • 鲍献文 1, 2
展开
  • 1. 中国海洋大学物理海洋教育部重点实验室, 山东 青岛 266100
  • 2. 中国海洋大学海洋与大气学院, 山东 青岛 266100
通讯作者：宋德海。Email:

作者简介：严聿晗(1993—), 男, 浙江省金华市人, 硕士研究生, 近海环流与物质输运。Email:

收稿日期: 2016-08-23

  要求修回日期: 2016-09-22

  网络出版日期: 2017-06-01

基金资助

国家重点基础研究发展计划(2015CB452905)

中国博士后科学基金第8批特别资助(2015T80742)

收起

Study on the tidal dynamics in Daya Bay, China — Part Ⅱ. The generation of double high waters and double-peak flood-current flows

  • YAN Yuhan , 1, 2 ,
  • WU Wen 2 ,
  • SONG Dehai , 1 ,
  • BAO Xianwen 1, 2
Expand
  • 1. Key Laboratory of Physical Oceanography, Ministry of Education, Ocean University of China, Qingdao 266100, China
  • 2. College of Oceanic and Atmospheric Sciences, Ocean University of China, Qingdao 266100, China
Corresponding author: SONG Dehai. E-mail:

Received date: 2016-08-23

  Request revised date: 2016-09-22

  Online published: 2017-06-01

Supported by

Major State Basic Research Development Program (2015CB452905)

China Postdoctoral Science Foundation (2015T80742)

Copyright

热带海洋学报编辑部
Fold

摘要

文章为大亚湾潮汐动力学系列研究论文的第二部分, 主要关注大亚湾双峰水位现象和涨潮流速双峰现象的产生机制。基于前人研究成果和数学解析方法, 得出在大亚湾海域水位的双峰现象主要是由以M2为代表的半日分潮与四分之一日分潮(如M4分潮)和六分之一日分潮(如M6分潮)共同作用造成的。并对产生双峰水位和涨潮流速双峰的条件进行了数学解析, 利用数值模拟结果发现, M2/M4分潮组合在大亚湾并不能产生双峰水位现象, 而M2/M6分潮组合只能在大亚湾东北的范和港产生双峰水位现象。相对而言, M2、M4和M6 3个分潮叠加的组合在双峰水位的产生范围和双峰间落差上都要大于上述2个分潮的组合。在大亚湾湾内区域, 涨潮流速双峰可以由M2/M4分潮组合, M2/M6分潮组合和M2/M4/M6分潮组合产生, M2/M4/M6分潮产生的涨潮流速双峰强度要比另外两组分潮组合大。

关键词： 大亚湾; 双峰水位; 涨潮流速双峰; 六分之一日分潮; 数值模拟

本文引用格式

严聿晗 , 武文 , 宋德海 , 鲍献文 . 大亚湾的潮汐动力学研究——Ⅱ.潮位和潮流双峰现象的产生机制[J]. 热带海洋学报, 2017 , 36(3) : 46 -54 . DOI: 10.11978/2016079

Abstract

This paper is the second part of our studies on tidal dynamics in Daya Bay (DYB), China. It illustrates the generation mechanism of double high waters and double-peak flood-current flows. Double high waters resulted from a subtle interaction between a semi-diurnal tide (M2) and higher harmonics (M4 and M6) in DYB. Based on previous studies, the conditions to produce double high waters and double-peak flood-current flows were found in this study by using an analytical method. The double high waters could be generated by combinations of M2/M6 tides (limited in the Fanhe Harbor) or M2/M4/M6 tides; however, the combination of M2/M4 tides failed to produce this unique phenomenon in DYB. Besides, the water falling range between two high waters generated by the combination of M2/M4/M6 tides was larger than that of M2/M6 tides, both in extension and in magnitude. The combinations of M2/M4, M2/M6 and M2/M4/M6 were all able to produce double-peak flood-current flows, but the magnitude of M2/M4/M6 triplet was larger than the other two pairs in DYB.

Key words： Daya Bay; double high waters; double-peak flood-current flows; sexta-diurnal tides; numerical simulation

潮汐水位和流速特征研究是海湾潮汐动力学的基本命题, 两者的变化特征会影响海湾水体交换和物质输运等其他物理过程, 进而对海湾生物地球化学过程产生重要影响。由本系列研究的第一部分(武文 等, 2017)可知, 在大亚湾海域, 大潮期间和小潮期间都可以观察到非常明显的双峰水位现象。与此同时, 在涨潮流期间, 双峰流速的现象也十分显著, 在发生两个涨潮流速峰值期间, 甚至出现落潮方向的流速, 这样的现象在之前的研究记录中十分少见。
潮波形变的一个重要现象就是海湾中高频振荡叠加半日分潮产生的双峰水位或者双谷水位现象。这种高频振荡可以是以秒或分为量级的海湾振荡(Bowers et al, 2013), 也可以是一个高频谐波分潮(Godin, 1993)。半日潮周期中双峰水位现象较为罕见, 例如咸平湾存在涨潮流速双峰现象, 但是却不存在双峰水位现象(Byun et al, 2006)。在欧洲的一些港口, 双峰水位的研究工作相对较为丰富(Godin, 1993)。例如, 在索伦特海峡出现的双峰水位对南安普顿港的形成与发展有很重要的作用(Airy, 1843; Doodson et al, 1941; Pugh, 1987);荷兰的登赫尔德港、美国马萨诸塞州的布扎兹湾和位于英格兰南海岸的斯沃尼奇湾也都观测到了双峰水位的现象(Pugh, 1987; Redfield, 1980; Godin, 1993)。通常来说, 双峰水位现象在大潮期间更为显著, 而在小潮期间则会出现被称为“停潮”或者“平潮”的静水现象(Bowers et al, 2013)。
鉴于大亚湾展现的双峰水位和涨潮流速双峰现象, 本文通过数学解析和数值模拟的方法进行深入研究, 初步阐释了半日分潮与其高频倍潮叠加能够产生潮位曲线和潮流曲线双峰结构的条件, 了解在大亚湾海域, 不同分潮组合可以产生双峰水位和涨潮流速双峰的分布特征。

1 研究背景

在2015年4月至5月间对大亚湾潮波系统进行了现场调查, 布置了2个潮位站和6船同步的全潮观测站(图1), 相关详细内容请参见本系列研究的第一部分(武文 等, 2017)。
Fig. 1 Bathymetry map of Daya Bay, with T1-T2 indicating tidal elevation stations and C1-C6 indicating tidal current stations

图1 大亚湾地形图^图中T1和T2为水位站, C1~C6为海流站

图2显示的是T1站和T2站实测的水位时间序列, 通过观察可以发现, T1站和T2站均发生了半日潮周期内的双峰水位现象, 此外, 位于湾顶附近的T1站双峰水位现象要明显强于靠近湾口的T2站双峰水位现象。值得注意的是, 在所发生的双峰水位现象中, 2个高峰的水位高度大部分情况下并不相同, 只在大潮的高高潮期间出现了水位高度相等的情况。由第一部分研究(武文 等, 2017)可知, 在6个实测流速站位中C3站的涨潮流速双峰现象最为明显(图3), 可见在2个涨潮流高峰期间, 随着时间的推移, 涨潮流速逐渐减小, 甚至出现了反向流速, 当反向流速不再增大后, 又向涨潮流方向逐渐增加, 直至出现第二个涨潮流的高峰。从观测数据来看, 在大亚湾海域, 水位和流速均稳定出现了双峰水位和涨潮流速双峰的现象。
Fig. 2 Observed water levels at Station T1 (black) and Station T2 (red)

图2 T1(黑色)和T2(红色)站实测水位时间序列^

Fig. 3 Observed current velocity at Station C3 for (a) u with eastward positive and (b) v with northward positive

图3 C3站的实测流速时间序列^a. 东西向流速(东为正); b. 为南北向流速(北为正)

2 分析与讨论

2.1 不同分潮对双峰水位现象的贡献

为了研究大亚湾内双峰水位的产生机制, 利用T1站所观测的数据进行调和分析得到调和常数, 并通过不同分潮的组合进行水位重构。考虑到潮时不对称效应对双峰水位产生的影响, 根据Song等(2011)的研究成果, 当2个分潮之间频率呈两倍关系, 或者3个分潮中的2个分潮频率之和等于另外一个分潮的频率时, 这些2个分潮和3个分潮的组合会对潮时不对称性产生影响, 表现为涨潮时间和落潮时间不一致, 发生潮波的形变现象。因此, 在对不同分潮组合进行水位重构过程中, 主要研究的是可能使潮波变形的组合。在重构过程中发现, 当只有M2分潮和M4分潮进行水位重构并不能产生双峰水位的现象, 但是加入M6分潮之后, 水位时间序列表现出双峰水位的特点, 如图4所示。由图5a可以看出, 由O1/K1/M2天文分潮组合, 只能解释大潮小潮的变化和潮位的日不等现象。从图5b可以看出, 在T1站, 其他四分之一日分潮(如: MS4)和半日潮的组合也不能产生双峰水位, 但是, 当相应地六分之一日分潮(如2MS6)加入上述组合之后, 重构的水位也出现了双峰水位的现象(图5c和5d)。
采用下面公式来统计不同的分潮对双峰水位影响的大小:
式中: SS反映不同分潮对实际观测水位所产生影响的大小, 不同分潮的SS越接近1, 则说明不同分潮影响观测水位的程度越大, 能解释实际观测水位的程度也越大; XP是重构后的水位时间序列; XO是实际观测的水位时间序列。
在T1站, 4个主要天文分潮(O1, K1, M2和S2)能够反映74.05% (SS = 0.7405)的实际观测水位。当在4大主要天文分潮之外加上M4分潮, SS增长到0.7964, 这意味着M4分潮可以解释5.59%的实际观测水位。与此同时, MS4分潮能反映3.55%的实际观测水位。当4大主要天文分潮之外加上M4和M6, SS增长到0.8379, 这意味着M6分潮能解释4.15%的实际观测水位。由于形成复合潮的频率关系条件, 2MS6分潮的主要来源有2个, 一个是M2分潮和MS4分潮的相互作用, 另一个是S2分潮和M4分潮的相互作用。由于2MS6分潮的加入, 使得天文分潮和M4分潮的SS增加了0.0357, 同时使得天文分潮和MS4分潮的SS增加了0.0354。相同的方法也被用于研究T2水位观测站观测到的水位时间序列, 其中4大主要天文分潮——M4分潮、MS4分潮、M6分潮和2MS6分潮对实际水位序列的贡献率分别为83.60%、3.20%、1.90%、0.66%和0.59%。显然, T2站天文分潮的作用要比T1站显著。由于T2站的四分之一日分潮和六分之一日分潮对观测水位的贡献度均小于T1站, 因此, T2站的水位双峰现象要弱于T1站的。
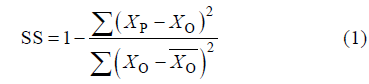
Fig. 4 The reproduced tidal-elevation curves at Station T1 by using combination of M2 tide and its overtides for (a) M2/M4, (b) M2/M6 and (c) M2/M4/M6

图4 T1站M2分潮与其倍潮的水位重构图^a. M2/M4; b. M2/M6; c. M2/M4/M6

Fig. 5 The reproduced tidal-elevation curves at station T1 by using combination of individual constituents for (a) O1/K1/M2, (b) M2/S2/MS4, (c) M2/MS4/2MS6 , and (d) S2/M4/2MS6

图5 T1站不同分潮组合的水位重构图^a. O1/K1/M2; b. M2/S2/MS4; c. M2/MS4/2MS6; d. S2/M4/2MS6

2.2 双峰水位的形成条件

前人研究认为双峰水位现象是由一个分潮(称之为“母潮”)与其高频倍潮叠加产生的, 只有倍潮与母潮的振幅比达到一定的标准才能在高潮时产生潮波的形变(Godin, 1993)。以M2分潮为例, M4、M6、M8、M10分别是其第2、3、4、5倍频率的谐波。依据Godin (1993)的理论, 能够产生双峰水位的条件是倍潮与母潮的振幅比大于其频率倍数平方的倒数, 也就是:
式中: 谐波倍潮振幅和母潮振幅的比值记为α; 谐波倍潮频率和母潮频率的比值记为k。根据上述公式可知, 只有当M4分潮的振幅超过M2分潮振幅的25%时, M4分潮才能产生双峰水位现象; 而M6分潮与M2分潮叠加能够产生双峰水位的条件是M6的振幅仅需超过M2振幅的1/9。频率倍数越高, 对倍潮振幅的要求就越低。在大亚湾T1站和T2站, M4分潮和M2分潮的振幅比分别为35.9%和26.7%, M6分潮和M2分潮的振幅比分别为29.4%和11.4% (武文 等, 2017), 均已超过式(2)的临界条件。但是从图4a和4b可以看出这两个频率的倍潮与母潮叠加均无法产生双峰水位现象, 这是因为根据Godin (1993)的理论要求母潮和倍潮的迟角差还要必须等于0°或180°, 因此, 式(2)给出的只是特殊的一类能够产生双峰水位现象的最低条件。
Bowers等(2013)曾经给出了一个适用性更广泛的公式:
式中: A为半日潮振幅(单位: m); 频率为ω (单位: °·s-1); B为其倍潮振幅; 频率为nω; n为高频倍潮频率相对低频潮频率的倍数; t′ 为2个最接近的水位高峰间的时间; C由下式计算:
式(3)以2个水位高峰之间的最小时间为依据, 更适合计算高频海湾振荡引起的双峰水位现象。但是式(3)在应用过程中忽略了潮波叠加形成的高阶项, 在一定程度上降低了其准确性。为此, 本文将从倍潮与母潮的振幅比与迟角差的关系入手, 解析双峰水位现象的产生条件。以M2分潮作为母潮, 与其倍潮的叠加可以表示为:
式中: η是水位(单位: m); ω是M2分潮的频率(单位: °·s-1); a1和a2分别是M2分潮与其谐波倍潮的振幅(单位: m); φ1和φ2分别是M2分潮与其谐波倍潮的迟角(单位: °); k是谐波倍潮和基本潮的频率的比值; t是时间(单位: s)。当出现双峰水位的时候, 水位关于时间的导数在一个M2潮周期内至少有4个根, 此时双峰水位时刻满足下列关系:
记α = a1/a2, Δφ = kφ1-φ2, θ = ωt+φ2/k, 由此上式可写作:
为了满足双峰水位产生条件, 上式等号左侧函数和等号右侧函数必须至少有4个交点。考虑临界的情况, 即临界情况时其中有两个交点合并为一个, 这个点是上述方程的一个极值点, 在极值点上, 方程关于θ的导数为0, 此时:
结合式(7)和式(8)可得:
此时, 给定k的值就能解出方程。
当k = 2的时候, 此时式(9)可写作:
式中: x = tanθ, y = tan(Δφ/2), 从而可以解得:
将式(11)带进式(7)和式(8)的平方和中, 并记ԑ = tan2θ, 可以得出临界状态时α和Δφ的关系, 当谐波倍潮和基本潮的频率的比值为2, 且α和Δφ满足式(12)时, 在这种情况下为出现双峰水位的临界状态, 如M2分潮为基本潮和M4分潮为谐波倍潮的情况。
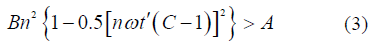
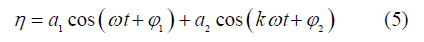
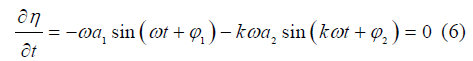
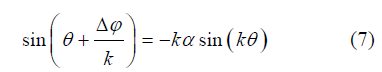
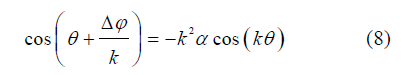
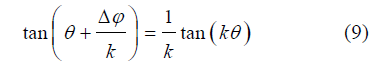
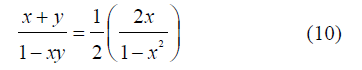
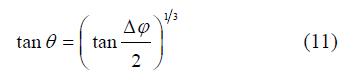
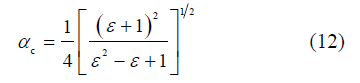
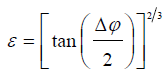式中: ; αc为临界状态下M2分潮与其谐波倍潮的振幅的比值。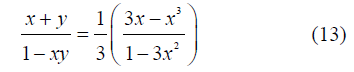
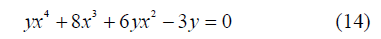
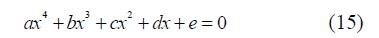
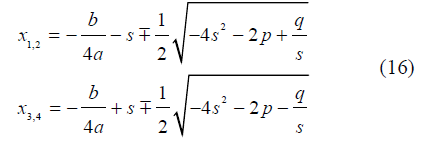
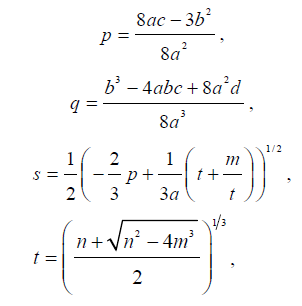
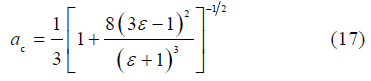
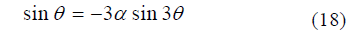
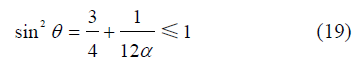
由此可知, 当产生双峰水位时, 要求α > αc。
当k = 3时, 式(9)可以写作:
式中: x = tanθ和y = tan(Δφ/3)。因此可以代数变换为:
当求解下面一元四次方程:
当a ≠ 0时, x1, x2, x3和x4为4个解。根据Ferrari一元四次求根公式:
式中:
式中: a、b、c、d、e均为常数; $m=c^2-3bd+12ae$; $n=2c^{3}-9bcd+27b^{2}c-72ace$。
对式(14)应用Ferrari一元四次求根公式, 通过数值解比较可知, tanθ = x1是所需的合理解(图6)。将其带入式(7)和式(8)的平方和中, 同时令ε = tan2θ, 可以求得当k = 3时, αc和Δφ之间的关系, 例如M2分潮和M6分潮的临界振幅比和相对相位之间的关系, 结果如下:
式中: ε = x12。
同样, 当产生双峰水位的时候, α应该大于αc。另外, 当y = 0时, 比如Δφ = 0时, 可得:
将sin3θ分解, 而且sinθ并不恒为零, 可以得出:
因此, 当Δφ = 0时, α≥1/3。
对于频率为母潮频率3倍以上的谐波倍潮, 它和母潮之间产生双峰水位的条件也可以用式(9)的计算得出, 但是计算过程会更为复杂。本文主要关注的是四分之一日分潮和六分之一日分潮, 因此, 只讨论k = 2和k = 3时的情况。为了表示双峰水位发生的情况和产生强度的大小, 本文用水位落差来量化双峰水位的强度, 水位落差越大说明双峰水位的现象越明显。水位落差是在一个半日潮周期内出现的2个高峰水位中相对较低的水位和离这个水位最近的低谷水位的高度差。图6a和图6b是在不同振幅比α和不同谐波之间迟角差Δφ的条件下, 计算出不同分潮组合的水位时间序列, 并通过水位时间序列读取其中水位落差的大小变化, 其中白色部分是不会发生双峰水位的情况(如图6c), 红色实线是由上述公式求得的双峰水位出现的临界状态的理论解, 彩色区域是使用数值方法的数值解。图6a的振幅比是M4分潮和M2分潮的组合, 图6b是M6分潮和M2分潮的组合。从图6a结果可知, 当振幅比和迟角差满足相应条件的时候, M2分潮和M4分潮相互作用也能产生双峰水位。当相对迟角在90°和270°时, 临界的α值达到最大, 此时α为0.50, 但是当相对迟角在0°和180°时, 临界α值达到最小值0.25,
这个结果与Godin (1993)的研究结果相一致。一般来说, 水位落差随着振幅比的增大而增大。当M2分潮迟角为0°和迟角差在0°到180°时, 双峰水位的第二个高峰更高(如图6d); 当迟角差在180°到360°之间时, 第一个高峰更高; 当迟角差等于180°时, 2个峰高度一致(图6e)。因此, 图6a呈现关于180°对称的形态。根据Song等(2011)研究表明: 在自然界中, 较大的 $a_{M_4}/a_{M_2}$非常少见, 在全球335个水位观测站中, $a_{M_4}/a_{M_2}$的最大值仅为0.5247。母潮和3倍频率谐波潮的相互作用比母潮和2倍频率谐波潮的相互作用更为复杂。由图6b可知, 当相对迟角为0°时, 临界的α值达到最大(1/3); 当相对迟角为180°时, 临界α值最小(1/9)。α最小临界值为1/9与Godin (1993)的结论相一致。比较图6a和图6b可以发现, 母潮和3倍频率谐波潮的相互作用与母潮和2倍频率谐波潮相比, 能够产生更大的水位落差。
Fig. 6 Two condition to produce double high waters (a) Conditions to produce double high waters by the combination of M2 and M4 tides. Color indicates water falling range (shown in meters), assuming = 0.35 m and = 0°. The red solid line gives the analytical critical solution. (b) is the same as (a), except for M2 and M6. (c) The tidal-elevation curve for /= 0.49 and -= 90°. (d) The tidal-elevation curve for /= 0.80 and -= 45°. (e) The tidal-elevation curve for /= 0.80 and -= 180°. The relationships between amplitude ratio and phase lag shown in (c), (d) and (e) corresponding to the black dots c, d and e in (a)

图6 两种双峰水位形成条件^a. 由M2/M4分潮造成的双峰水位的形成条件。= 0.35m、= 0°, 红线代表的是临界条件的解析解; 图中黑点c、d、e分别对应图c、d、e中的振幅比和迟角差关系。b. 由M2/M6分潮造成的双峰水位的形成条件。c. 当/= 0.49、-= 90°时的水位序列图; d. 当/= 0.80、-= 45°时的水位序列图; e. 当/= 0.80、-= 180°时的水位序列图

为了分析大亚湾出现双峰水位的区域的分布情况, 将上述研究结果用于本系列研究第一部分(武文等, 2017)所使用的数值模式中, 利用模式中各格点水位时间序列求得的调和常数, 计算不同分潮组合水位时间序列, 读取其中的水位落差。图7显示了大亚湾湾口至湾顶各处水位落差结果。图7a是由M2/M6分潮组合造成的水位落差计算结果; 图7b是由M2/M4/M6分潮组合造成的水位落差计算结果, 白色区域表明M2/M6分潮组合在该区域不能产生双峰水位现象, 由此可见, M2分潮和M6分潮的相互作用能产生双峰水位, 但是主要发生在范和港。研究过程中发现, 在大亚湾海域, M2分潮和M4分潮的相互作用并不能产生双峰水位现象, 然而在M2分潮和M4分潮的相互作用下, 加上M6分潮的作用后, 在大辣甲以北的海湾都能发生双峰水位现象, 并且自湾口向湾顶双峰水位的强度逐渐变大, 强度最大的位置在范和港附近。值得注意的是, 从图7a和图7b的比较来看, M2/M4/M6分潮组合与M2/M6分潮组合相比, M4分潮的加入不仅能使产生双峰水位的范围扩大, 还能大幅提升所产生的双峰水位的强度大小。

2.3 大亚湾涨潮流速双峰现象

从本系列研究的第一部分(武文 等, 2017)以及图3可以看出, 在大亚湾海域可以观察到涨潮流速双峰的现象。与研究双峰水位方法类似, 应用前面所述公式, 利用武文等(2017)使用的数值模型结果, 计算了大亚湾湾口至湾顶M2分潮及其倍潮之间的
Fig. 7 The distribution of water falling range (units: m) in Daya Bay by using combination of individual constituents for (a) M2/M6 and (b) M2/M4/M6

图 7 大亚湾内M2/M6(a)和M2/M4/M6(b)所产生水位落差的分布图

振幅比α与能产生涨潮流速双峰的临界αc的差值, 计算振幅比使用各点流速潮流椭圆主轴长度, 计算结果如图8所示, 计算结果大于0的区域表示可以发生涨潮流速双峰, 小于0时则不能发生涨潮流速双峰。从图8中可以看出, 在大亚湾湾内, M2/M4分潮组合(图8a)和M2/M6分潮组合(图8b)均可以产生涨潮流速双峰的现象。值得注意的是, 因为求得的数值仅仅为M2分潮及其倍潮之间的振幅比α与能产生涨潮流速双峰的临界αc的差值, 而双高峰的强度还与2个分潮之间的迟角差有关, 所以图8并不能反映大亚湾双高峰发生的强度分布。
为了量化涨潮流速双峰现象的强度, 参考水位落差的定义, 将母潮的涨潮流方向设为正方向, 其他分潮流流速都投影到母潮的涨潮流方向上, 将涨潮流期间2个涨潮流方向的高峰流速中相对较小的流速和离此流速最近的谷值流速相差的绝对值作为判断流速所发生的双峰现象的强度, 称为流速落差。
Fig. 8 (a) Difference between/and critical /to produce double-peak flood-current flow (positive indicates the capability to produce double-peak flood- current flow). (b) Same as (a), except for M2 and M6

图8 利用模式结果计算/和临界/的差(a)和利用模式结果计算/和临界/的差(b)^数值为正代表可以产生涨潮流速双峰; 图中黑色实线是数值为0的等值线

图9显示的是在大亚湾内M2/M4分潮组合(图9a)、M2/M6分潮组合(图9b)和M2/M4/M6分潮组合(图9c)所产生的涨潮流速双峰的流速落差大小的分布图。值得注意的是, 在大亚湾内呈现白色区域的主要是M2分潮和倍潮(即M4分潮和M6分潮)的潮流椭圆主轴方向相差15°以上的区域(为了便于计算, 当主轴之间的方向差值在15°以内, 认为主轴方向是一致的)。还有部分区域是由于水深过浅, 模拟过程中会出现潮滩露出水面的情况, 无法进行调和分析。由图9中a、b、c对比可见, 这3组分潮所产生的流速落差分布较为类似, 与M2/M6分潮引起的双峰现象相比, 由M2/M4分潮引起的双峰现象流速落差较小。此外, 流速落差在范和港等潮汐通道和沿岸或环岛浅水区域强度大。M2/M4/M6分潮组合所产生流速的双峰强度要比M2/M4分潮组合和M2/M4分潮组合所产生的强度要大, 这与水位重构和水位落差分布结论类似。
Fig. 9 The distribution of Current Difference Range (units: m·s-1) in Daya Bay by using combination of individual constituents for (a) M2/M4, (b) M2/M6 and (c) M2/M4/M6

图 9 大亚湾M2/M4 (a)、M2/M6 (b)和M2/M4/M6 (c)所产生的流速落差分布图

3 结论

本文作为大亚湾潮汐动力学系列研究论文的第二部分, 在第一部分研究的基础上, 进一步探究了双峰水位和涨潮流速双峰现象的产生机制。依据前人研究成果, 从倍潮与母潮的振幅比与迟角差的关系入手, 通过数学解析, 基本阐明双峰水位和涨潮流速双峰的形成机制。利用本系列研究第一部分所构建的数值模型, 分析得出在大亚湾海域不同分潮组合的双峰水位和涨潮流速双峰发生区域的分布, 并通过水位落潮和流速落差来刻画其强度, 并得出如下结论:
1) 大亚湾产生的双峰水位和涨潮流速双峰是由M2分潮与其倍潮相互叠加产生的。从水位重构的过程来看, 在T1站, M2分潮和M4分潮共同叠加并不能产生双峰水位, 但是, 在M6分潮的帮助下, 可以产生双峰水位现象。
2) 对M2作为母潮和其倍潮之间产生双峰水位和涨潮流速双峰的数学解析研究得出了M2/M4分潮组合和M2/M6分潮组合可以产生双峰现象的振幅比与迟角差之间的关系。同时发现M2/M6分潮组合产生的双峰现象强度要大于M2/M4分潮组合产生的双峰现象的强度。
3) 在大亚湾, M2/M4分潮组合并不能产生双峰水位现象, M2/M6分潮组合产生的双峰水位现象主要在范和港。然而, M2/M4/M6分潮组合产生的双峰水位现象的范围要大得多, 可以到大辣甲以北海域, 双峰的强度从湾口到湾顶逐渐增强, 而且M2/M4/M6分潮组合产生的双峰水位现象强度比M2/M6分潮组合产生的强度要大。
4) 在大亚湾, M2/M4分潮组合、M2/M6分潮组合和M2/M4/M6分潮组合都可以产生涨潮流速双峰现象。在大亚湾湾内, 以上3个分潮组合所发生的双峰现象的强度分布是相似的, 与潮位的研究类似, M2/M4/M6分潮组合产生的涨潮流速双峰现象强度比M2/M4分潮组合和M2/M6分潮组合所产生的强度大。

The authors have declared that no competing interests exist.

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
武文, 严聿晗, 宋德海, 2017. 大亚湾的潮汐动力学研究——I. 潮波系统的观测分析与数值模拟[J]. 热带海洋学报, 36(3): 34-45.

WU WEN, YAN YUHAN, SONG DEHAI, 2017. Study on the tidal dynamics in Daya Bay, China - Part I. Observation and numerical simulation on tidal dynamic system[J]. Journal of Tropical Oceanography, 36(3): 34-45 (in Chinese).

[2]
AIRY G B, 1843. On the laws of individual tides at Southampton and at Ipswich[J]. Philosophical Transactions of the Royal Society of London, 133: 45-54.

[3]
BOWERS D G, MACDONALD R G, MCKEE D, et al, 2013. On the formation of tide-produced seiches and double high waters in coastal seas[J]. Estuarine, Coastal and Shelf Science, 134: 108-116.

[4]
BYUN D-S, CHO Y-K, 2006. Double peak-flood current asymmetry in a shallow-water-constituent dominated embayment with a macro-tidal flat[J]. Geophysical Research Letters, 33(16): L16613.

[5]
DOODSON A T, WARBURG H D, 1941. Admiralty manual of tides[M]. London: H. M. Stationery Office: 270.

[6]
GODIN G, 1993. An investigation of the phenomenon of double high water or double low water at some harbours[J]. Deutsche Hydrografische Zeitschrift, 45(2): 87-106.

[7]
PUGH D T, 1987. Tides, surges, and mean sea-level[M].J. Wiley: 472.

[8]
REDFIELD A C, 1980. The tides of the waters of New England and New York[M]. Woods Hole: Woods Hole Oceanographic Institution: 108.

[9]
SONG DEHAI, WANG XIAOHUA, KISS A E, et al, 2011. The contribution to tidal asymmetry by different combinations of tidal constituents[J]. Journal of Geophysical Research: Oceans, 116(C12): C12007.

Options
文章导航

/

〈 〉