检索
E-mail
RSS

作者投稿 主编审稿 专家审稿 远程编辑

热带海洋学报 >

2017 , Vol. 36 >Issue 4: 35 - 47

DOI: https://doi.org/10.11978/2016118

利用理想模型实验研究涡旋碰撞海岛的过程*

  • 魏子淋 , 1, 2 ,
  • 薛惠洁 , 1, 3 ,
  • 覃慧玲 1 ,
  • 耿兵绪 1
展开
  • 1. 热带海洋环境国家重点实验室(中国科学院南海海洋研究所), 广东 广州510301
  • 2. 中国科学院大学, 北京100049
  • 3. 缅因大学, 海洋科学学院, 美国缅因州04469
通讯作者:薛惠洁。Email:

作者简介：魏子淋(1992—), 男, 湖北省宜昌市人, 硕士研究生, 主要从事中尺度涡研究。E-mail:

收稿日期: 2016-11-17

  要求修回日期: 2017-04-07

  网络出版日期: 2017-07-26

基金资助

国家自然科学基金委基金(41476013)

中国科学院战略性先导科技专项(XDA11010304)

收起

Using idealized numerical experiment to study an eddy colliding with an island*

  • WEI Zilin , 1, 2 ,
  • XUE Huijie , 1, 3 ,
  • QIN Huiling 1 ,
  • GENG Bingxu 1
Expand
  • 1. State Key Laboratory of Tropical Oceanography (South China Sea Institute of Oceanology, Chinese Academy of Sciences), Guangzhou 510301, China
  • 2. University of Chinese Academy of Sciences, Beijing 100049, China
  • 3. School of Marine Sciences, University of Maine, the State of Marine 04469, USA
Corresponding author: XUE Huijie. Email:

Received date: 2016-11-17

  Request revised date: 2017-04-07

  Online published: 2017-07-26

Supported by

National Natural Science Foundation of China (41476013)

Chinese Academy of Sciences Strategic Leading Science and Technology Projects (XDA11010304)

Copyright

热带海洋学报编辑部
Fold

摘要

利用区域海洋模式(regional ocean modeling system, ROMS)构建理想模型实验来探讨f-平面上涡旋碰撞海岛的过程。结果表明, 在理想模型设定条件下, 当北半球的反气旋式涡旋以一定速度与尺度相当的海岛发生正面碰撞时, 反气旋式涡旋的部分涡度会从涡旋移动方向的左侧“绕”过海岛形成一个新的反气旋式涡旋, 同时, 在碰撞过程中, 会在移动方向碰撞点的右侧形成一个新的气旋式涡旋。在碰撞过程中, 海岛主要起阻挡作用, 产生碰撞方向水流速度的切变导致涡度梯度的增加, 从而使涡旋结构中的正负涡度发生聚集, 导致涡旋结构的改变。

关键词： 涡旋; 海岛; 碰撞; ROMS; 理想实验

本文引用格式

魏子淋 , 薛惠洁 , 覃慧玲 , 耿兵绪 . 利用理想模型实验研究涡旋碰撞海岛的过程*[J]. 热带海洋学报, 2017 , 36(4) : 35 -47 . DOI: 10.11978/2016118

Abstract

In this study, we used the Regional Ocean Modeling System (ROMS) to investigate the interaction of eddy with an island by constructing an idealized numerical experiment on the f-plane. The results are as follows. Under the specified condition of the idealized experiment, when the anticyclonic eddy in the Northern Hemisphere collides with the island of a comparable size, part of the anticyclonic eddy's vorticity bypasses the island from the left side of the moving eddy to form a new anticyclonic eddy. At the same time, a new cyclonic eddy forms on the right side of the eddy. In the colliding process, the island mainly acts as a blocking object to increase the vorticity gradient near collision point and to aggregate the positive and negative vorticity related to the eddy leading to modification of the eddy structure.

Key words： eddy; island; collision; ROMS; idealized experiment

涡旋是海洋中无处不在的现象(Robinson, 1983), 就算是长期被认为是弱流区的中大洋区域, 也存在着中尺度涡(管秉贤 等, 2006; Chelton et al, 2011)。中尺度涡是海洋运动的重要形式, 它的生消也是大尺度环流季节调整的一个基本方式(王东晓, 1996)。中尺度涡在运动过程中不可避免地会遇到海洋中的各种地形。本文主要关心其在碰撞到岛屿后会发生哪些变化, 因为中尺度涡对热量、水团、动量和生物化学物质的运输有重要作用(Xiu et al, 2010; Chen et al, 2012)。
早期的一些研究探讨了涡旋与斜坡的作用(Nof, 1983; Smith et al, 1983; Thierry et al, 1999)。通过对位势涡度的分析, 指出了行星β效应和地形β效应的共同作用, 并解释了在β平面上气旋涡会有极向运动、反气旋涡会有朝赤道运动的趋势, 以及这两类涡旋均有西向传播特征的原因。但涡旋与海岛的作用和斜坡是不同的, 而且更复杂(Herbette et al, 2003)。
Arhan等(1999)、Schouten等(2000)发现某些阿古拉斯流涡(Agulhas rings)在海山的作用下会分解为多个涡旋。也有一些学者研究了地中海的涡旋与海山之间的相互作用(Simmons et al, 2000; Wang et al, 2003a), 其中Simmons等(2000)从角动量守恒的角度探讨了此问题, 认为涡旋中角动量的积分守恒比能量守恒制约更强。
现实中的海岛对涡旋的作用不可避免地受到各种因素影响, 比如不规则的海岛, 变化的流速, 地理位置等, 因此以往研究中对特定海区涡旋与海岛相互作用的结论缺少普适性。有不少研究通过实验室实验来研究海岛对涡旋的作用。Adduce等(2004)、Cenedese等(2005), Cenedese(2002)采用实验室模拟研究了海岛对中尺度涡旋的作用, 他们将涡旋的移动分为自主传播与在背景流作用下传播两类来探讨, 其中自主传播是用上面提到的地形β效应代替行星β效应来实现涡旋的移动。该研究指出了两类不同传播情况下涡旋分解为两个涡旋的条件: 对于自主传播的气旋式涡旋(北半球), 其碰撞海岛时需要更靠近海岛的左侧(涡旋移动方向的左侧)部分; 对于背景流推动的涡旋, 碰撞点则可以比自主传播的气旋式涡旋(北半球)稍偏右一些。由于背景流推动的涡旋的分解条件比自主传播涡旋的分解条件更宽松, 因此他们认为背景流的作用能加强涡旋的分解。Andres等(2013)比较了实验室结果和冲绳岛附近的现场观测, 指出虽然实验装置和真实海洋有明显的不同, 包括简化的地形, 简化的涡旋垂直结构, 和本地强迫等, 然而就低阶近似而言, 二者相对一致, 即在实验室产生的过程与真实海洋有一定相似性。
也有学者通过各种数值实验研究了涡旋与海山的碰撞过程。Van Geffen等(2000)采用二维数值模型来研究β平面条件下涡旋碰撞海山时对涡旋的影响, 认为碰撞过程主要和以下因素有关: 碰撞发生于南半球还是北半球、海山的侧面尺度与涡旋尺度的相对大小。海山越大或者离赤道越远, 海山对涡旋的作用越剧烈, 越会导致涡旋分解。
Herbette等(2003)运用层化模型来分析表层强化的反气旋式涡旋遇到海山时发生的作用。他们的敏感性实验涉及的不同参数包括涡旋和海山之间的距离、涡旋半径、海山半径、海山高度和层化。该研究表明, 海山对涡旋的侵蚀常常会导致涡旋的分解。当涡旋与海山相遇后, 原来的反气旋式涡旋结构变为偶极子结构, 有时也会分解为两个以上的结构。涡丝有时也会分离为两个以上的结构。
McWilliams等(1979)运用垂直模态(vertical mode)探讨了一个理想涡旋的演化过程, 认为涡旋振幅衰减率(vortex amplitude decay rate)主要是由摩擦系数控制, 而不是频散(dispersion)。结合Simmons等(2000)的观点, 或许可以理解为, 涡旋在整个生命周期均受到摩擦力的作用, 从几个月甚至几年的生命周期来看, 涡旋的消亡主要是由摩擦力主导的, 但由于涡旋碰撞海山的时间往往较短, 在此期间, 涡旋在一定程度上是角动量守恒的。
南海较其他边缘海而言较大且较深, 具备了小大洋的一些特征。强季风、入流所驱动的南海环流在β效应和地形的作用下导致西边界流强化(Chen et al, 2014)。强流在经过群岛时可诱导出很多涡旋(Calil et al, 2008)。南海的中尺度涡尤其活跃, 最大涡旋动能位于越南以东海域(Cheng et al, 2010)。南海中存在着诸多岛屿, 故选择南海涡旋作为本研究设置数值实验中涡旋的参考。综合前人研究(Wang et al, 2003b; 林鹏飞 等, 2007; Chow et al, 2008; Xiu et al, 2010; 陈更新, 2010), 由于卫星资料时间的限制, 对于南海中尺度涡的统计研究一般从1993年开始, 半径范围一般认为在50~250km之间, 但对于半径峰值, 由于统计年份、位置及资料的不同, 各研究并不一致, 综合而言, 峰值在100km左右; 涡旋生命周期多数在180d以内, 近半数为30~60d; 移动速度范围为-9~3cm·s-1(“-”代表西向), 且大部分涡旋均具有西向传播的特征; 大部分统计研究均显示反气旋涡数目要比气旋涡多。
由于前人研究中的各个数值模型实验中对涡旋结构的设定各不一样, 且研究海区不同, 背景流的设定, 海岛或海山的地形设定也不同, 故目前对于涡旋碰撞海岛的过程还没有系统完整的认识, 需要有大量敏感性理想实验来探讨不同情况下海岛对涡旋的影响, 这部分研究将在后续的工作中进一步展开。本研究主要就一个涡旋遇上尺度相当的海岛的理想实验来揭示海岛对涡旋的作用, 以及碰撞后诱导出新涡旋的物理机制。

1 模拟区域及初始场设置

本文的数值实验采用的是区域海洋模式系统(regional ocean model system, ROMS)。ROMS是一个自由海表面、地形跟踪、原始方程海洋模型, 其使用的坐标系为S—坐标系(stretched terrain- following coordinates), 这种坐标系能够较好地描述地形对流场的影响, 在温跃层、底边界层等地方的分辨率也可随需求增高。

1.1 模型基本设置介绍

模型区域的东西及南北方向距离分别为1272km和660km; 模型北边为固体边界, 东、西、南边为开边界; 东西、南北向水平分辨率分别为3.533km和3.667km, 足以分辨出中尺度涡。除海岛外, 水深统一设为1500m, 垂直方向分为40层, 非均匀分层。本文主要关注表层附近的流场情况, 故在表层附近的垂向分层要密集很多, 其中控制表层和底层密集程度的参数分别取值为: θS=6.5, θB=2.0。当水深为-1500m时, 500m以上的垂直分层为29层。模型总积分时间为60d, 内模时间步长为10s, 外模时间步长为200s。每隔4h输出一次模型结果。
理想实验是在ROMS模式自带的海山案例下修改得到的。在海山案例基础上修改温盐平流格式为正定平流格式(TS_MPDATA), 且加入了三阶迎风分离示踪格式(UV_U3ADV_SPLIT), 以减少地形追随坐标下平流计算中的虚假扩散。由于本研究目的是探讨涡旋碰撞海岛的物理机制, 故不考虑盐度的影响。二维U、V动量的侧边界条件设置为: 西侧为辐射逼近型(radiation and nudging), 南侧为辐射型(radiation), 东侧为夹紧型(clamped)。其他变量的开边界条件都设置为辐射型(radiation)。为了保持计算区域中的水体体积守恒, 故在东、西、南三处开边界又使用了体积守恒限制。二次阻力系数(quadratic drag coefficient)为3×10-3; 海底粗糙度(bottom roughness)为2×10-2m, 海表粗糙度(surface roughness)为2×10-2m; 固体边界上, 滑动系数(slipperiness parameter)设置为-1.0(no slip), 即为无滑动边界条件; 水平扩散系数(horizontal diffusion of tracer)和水平黏性系数(horizontal viscosity coefficient)均设置为0。该实验是在f-平面假设下进行的, 具体取值参见附录, 相当于北半球15°附近的科氏参数(约为3.7632×10-5s-1), 是南海的典型纬度。

1.2 涡旋速度场、温度场及海岛设置

Zhang 等(2013)通过对全球卫星高度计资料和Argo浮标数据的综合分析, 得到了一个关于涡旋的标准化三维结构, 且具有很好的效果(Zhang et al, 2014), 故本文利用该公式构造一个典型涡旋来研究此问题。涡旋速度场和温度场的控制公式的具体推导过程如下文所示。由于该涡旋结构是一个全球统一的三维结构, 因此在构造背景场及利用该公式构造理想涡旋时还需要一个参考对象。综合引言中对南海涡旋的研究, 最终选择本研究模拟涡旋的半径为50000.0m, 深度为500m。本研究中还加入了背景流, 其流速大小为0.2m·s-1, 方向沿着x轴的负方向, 主要是为了加快模型积分。海岛在海表处的半径为38866.7m, 比涡旋半径略小, 保证了涡旋碰撞海岛过程中海岛作用足够明显, 且涡旋能够在背景流的作用下以较强的速度撞向海岛。海岛的设置请见下文。对于涡旋深度, Williams等(2011)曾对全球涡旋分布的深度有过统计, 其中南海涡旋的深度均较浅。Xiu等(2010)也曾对南海涡旋的深度做过分析, 指出涡旋的深度集中在500m以内。

1.3 涡旋速度场及温度场推导

Zhang等(2013)指出涡旋标准化后的压强异常场结构$\tilde{P}\left( \tilde{r}\text{, }z \right)$可用下述公式(1)来描述:
$\tilde{P}(\tilde{r},z)=R(\tilde{r})\text{ }\!\!\cdot\!\!\text{ }H(z)$ (1)
其中$R\left( {\tilde{r}} \right)$与$H\left( z \right)$分别是中尺度涡压强异常场的径向结构函数与垂向结构函数,计算过程如下所示:
$R(\tilde{r})=(1-\frac{{{{\tilde{r}}}^{2}}}{2})\cdot {{\text{e}}^{-\frac{{{{\tilde{r}}}^{2}}}{2}}}$ (2)
$H({{z}_{\text{s}}})={{H}_{0}}\cdot \sin (k{{z}_{s}}+{{\theta }_{0}})+{{H}_{\text{ave}}}$ (3)
其中$\tilde{r}=r/{{R}_{0}}$, r为到涡旋中心的水平辐射距离, R0为涡旋的半径; z为垂向坐标, 拉伸的垂向坐标${{z}_{\text{s}}}=\int_{0}^{z}{(N/f)\text{d}z}$, 其中N为浮动频率, f为科氏参数,; H0、k、θ0、Have均为待定系数。
为了简化描述涡旋的公式, 取浮动频率N为定值, 不随深度变化。为方便计算, 对于公式(3), 深度为500m的涡旋取H0=2/3, Have=2/3, N=0.000912, k=π/18000, f=3.8×10-5s-1, 则(k·N)/f=π·4/3000。图1为500m以上涡旋的垂向结构函数H(z)的分布图, 对比Zhang等(2013)文章中的图3, 结果类似, 故对于描述涡旋垂直结构的公式(3)的具体参数取值符合Zhang等(2013)的定义。
Fig. 1 H and z diagram of eddy whose depth is 500m

图1 深度为500m涡旋的H和z关系图

由上述分析, (1)式可变为
$\tilde{P}({{x}_{1}},{{y}_{1}},{{z}_{1}})=(1-\frac{x_{1}^{2}+y_{1}^{2}}{2R_{0}^{2}})\cdot {{\text{e}}^{-\frac{x_{1}^{2}+y_{1}^{2}}{2R_{0}^{2}}}}\cdot \left[ \frac{2}{3}\cdot \sin (\frac{4}{3000}\text{ }\!\!\pi\!\!\text{ }\cdot {{z}_{1}}+\frac{\text{ }\!\!\pi\!\!\text{ }}{6})+\frac{2}{3} \right]$(4)
其中x1, y1, z1为以表层涡旋中心为坐标原点的笛卡尔坐标系下的坐标, 单位均为m。
假设涡旋的真实压强场可以由下面的公式得到: $P({{x}_{1}},{{y}_{1}},{{z}_{1}})={{P}_{0}}\cdot \tilde{P}({{x}_{1}},{{y}_{1}},{{z}_{1}})+\overline{P}$, 这里$\overline{P}$为多年季节平均, 即气候态数据; P0为涡旋强度。由于该理想实验除了匀速的背景流之外, 只有涡旋的信号, 即$\overline{P}$ 与x1、y1无关, 但为了背景场温度在垂向上与实际海洋类似, $\overline{P}$与z1有关, 即$\overline{P}({{z}_{1}})$。则描述涡旋的压强场为:
$P({{x}_{1}},{{y}_{1}},{{z}_{1}})={{P}_{0}}\left\{ (1-\frac{x_{1}^{2}+y_{1}^{2}}{2R_{0}^{2}})\cdot {{\text{e}}^{-\frac{x_{1}^{2}+y_{1}^{2}}{2R_{0}^{2}}}}\cdot \left[ \frac{2}{3}\cdot \sin (\frac{4}{3000}\text{ }\!\!\pi\!\!\text{ }\cdot {{z}_{1}}+\frac{\text{ }\!\!\pi\!\!\text{ }}{6})+\frac{2}{3} \right] \right\}+\overline{P}({{z}_{1}})$ (5)
由地转平衡公式$\left\{ \begin{matrix}0=-\frac{1}{\rho }\frac{\partial P}{\partial x}+fv \\0=-\frac{1}{\rho }\frac{\partial P}{\partial y}-fu \\\end{matrix} \right.$结合(5)式可得速度场为:
$\left\{ \begin{matrix} u=-\frac{{{P}_{0}}}{\rho f}\left[ \frac{y_{1}^{3}+{{y}_{1}}x_{1}^{2}-4{{y}_{1}}R_{0}^{2}}{2R_{0}^{4}} \right]{{\text{e}}^{-\frac{x_{1}^{2}+y_{1}^{2}}{2R_{0}^{2}}}}\left[ \frac{2}{3}\sin (\frac{4}{3000}\text{ }\!\!\pi\!\!\text{ }{{z}_{1}}+\frac{\text{ }\!\!\pi\!\!\text{ }}{6})+\frac{2}{3} \right] \\ v=\frac{{{P}_{0}}}{\rho f}\left[ \frac{x_{1}^{3}+{{x}_{1}}y_{1}^{2}-4R_{0}^{2}{{x}_{1}}}{2R_{0}^{4}} \right]{{\text{e}}^{-\frac{x_{1}^{2}+y_{1}^{2}}{2R_{0}^{2}}}}\left[ \frac{2}{3}\sin (\frac{4}{3000}\text{ }\!\!\pi\!\!\text{ }{{z}_{1}}+\frac{\text{ }\!\!\pi\!\!\text{ }}{6})+\frac{2}{3} \right] \\ \end{matrix} \right.$(6)
再由静力方程$\frac{\partial P}{\partial z}=-\rho g$及状态方程$\rho ={{\rho }_{0}}(1-\alpha T)$可推导出温度场的公式(7)。式(7)中取α=3×10-4℃-1, f=3.8×10-5s-1, ρ0=1025kg·m-3, 则温度场为公式(8)。通过调试, 最终确定北半球反气旋式涡旋(气旋涡类似考虑, 不再阐述)的速度场和温度场(水深为500m以内)的具体表达式为公式(9)、(10)和(11)。
$T=\frac{1}{\alpha }+\frac{1}{\alpha {{\rho }_{0}}g}\cdot \left\{ {{P}_{0}}\cdot (1-\frac{x_{1}^{2}+y_{1}^{2}}{2R_{0}^{2}}){{\text{e}}^{-\frac{x_{1}^{2}+y_{1}^{2}}{2R_{0}^{2}}}}\cdot [\frac{2}{3}\cdot \frac{4}{3000}\text{ }\!\!\pi\!\!\text{ }\cos (\frac{4}{3000}\text{ }\!\!\pi\!\!\text{ }{{z}_{1}}+\frac{\pi }{6})]+\overline{P}({{z}_{1}})' \right\}$ (7)
$T=\frac{8}{9000}\text{ }\!\!\pi\!\!\text{ }\cdot \frac{{{P}_{0}}}{\alpha {{\rho }_{0}}g}\cdot \left\{ (1-\frac{x_{1}^{2}+y_{1}^{2}}{2R_{0}^{2}}){{\text{e}}^{-\frac{x_{1}^{2}+y_{1}^{2}}{2R_{0}^{2}}}}\cdot [\cos (\frac{4}{3000}\text{ }\!\!\pi\!\!\text{ }{{z}_{1}}+\frac{\text{ }\!\!\pi\!\!\text{ }}{6})]+C({{z}_{1}}) \right\}$ (8)
$\begin{align} & u=-5\times {{10}^{4}}\cdot (\frac{y_{1}^{3}+{{y}_{1}}x_{1}^{2}-4{{y}_{1}}R_{0}^{2}}{2R_{0}^{4}})\cdot {{\text{e}}^{-\frac{x_{1}^{2}+y_{1}^{2}}{2R_{0}^{2}}}}\cdot [\frac{2}{3}\cdot \sin (\frac{4}{3000}\text{ }\!\!\pi\!\!\text{ }\cdot {{z}_{1}}+\frac{\text{ }\!\!\pi\!\!\text{ }}{6})+\frac{2}{3}] \\ & \\ \end{align}$ (9)
$v=5\times {{10}^{4}}\cdot (\frac{x_{1}^{3}+{{x}_{1}}y_{1}^{2}-4{{x}_{1}}R_{0}^{2}}{2R_{0}^{4}})\cdot {{\text{e}}^{-\frac{x_{1}^{2}+y_{1}^{2}}{2R_{0}^{2}}}}\cdot [\frac{2}{3}\cdot \sin (\frac{4}{3000}\text{ }\!\!\pi\!\!\text{ }\cdot {{z}_{1}}+\frac{\text{ }\!\!\pi\!\!\text{ }}{6})+\frac{2}{3}]$ (10)
$T=1.8047\times \cos (\frac{4}{3000}\text{ }\!\!\pi\!\!\text{ }\cdot {{z}_{1}}+\frac{\text{ }\!\!\pi\!\!\text{ }}{6})\cdot [-\frac{x_{1}^{2}+y_{1}^{2}}{2R_{0}^{2}}\cdot {{\text{e}}^{^{-\frac{x_{1}^{2}+y_{1}^{2}}{2R_{0}^{2}}}}}+{{\text{e}}^{^{-\frac{x_{1}^{2}+y_{1}^{2}}{2R_{0}^{2}}}}}+7{{\text{e}}^{5{{z}_{1}}/1000}}+1.6]+10$ (11)
公式(7)—(11)中0≥z1≥-500m。
由于涡旋深度为500m, 而该理想实验的最大水深为1500m, 故还需给定在水深500~1500m的温度场: $T=60\cdot {{\text{e}}^{5{{z}_{1}}/1000}}+10-60\cdot {{\text{e}}^{-5\times 0.5}}$ (12)
其中-500m>z1≥-1500m。对应的速度场为0。
图2显示深度为500m, 半径R0为50km的涡旋温度剖面图和相应的速度场, 该温度图接近南海温度的垂向分布。
Fig. 2 Temperature distribution(a) and corresponding u-velocity distribution(b) of eddy whose depth and radius is 500m and 50km, respectively

图2 深度为500m, 半径R0为50km的涡旋温度剖面图(a)及相应的u速度剖面图(b)

1.4 海岛设置

海岛公式如下所示:
${{z}_{2}}=1780\times ({{1.15}^{a}})-1500$ (13)
$a=-[{{(\frac{{{x}_{2}}}{30000})}^{2}}+{{(\frac{{{y}_{2}}}{30000})}^{2}}]$ (14)
其中x2、y2、z2是以海面海岛中心为坐标原点的笛卡尔坐标系下的坐标。z2中大于-100m的值设定为陆地点。图3为海岛的三维地形图以及等深线图。
Fig. 3 Three dimensional topographic map of the island

图3 涡旋与海岛作用实验三维地形图

2 实验结果分析

2.1 反气旋式涡旋(北半球)

通过表层(-1m)涡度水平空间分布图(图4)可看出, 反气旋式涡旋大约在12d时碰撞到海岛(模式运行不到10d就已达到相对稳定状态)。反气旋式涡旋中心是负涡度(蓝色), 但在其外围一定范围内被较强的正涡度(橘黄色)包围(图4a), 这由Zhang等(2013)的文章中也可看出此现象: 涡旋由中心向外是有一个速度的反向, 若涡旋为北半球的反气旋式涡旋, 那么这种速度反向会在涡旋外围形成一个环状的正涡度。这也是Zhang等(2013)给的涡旋公式不同于其他涡旋公式的重要原因。当涡旋靠近海岛时, 在涡旋与海岛相切点的北侧区域正涡度有显著增加(图4b、c、e、f), 从而诱导出一个气旋式涡旋(图4c、d), 本研究将其称之为C涡旋; 而在涡旋与海岛相切点的南侧区域并没有出现正涡度聚集, 而是出现了涡旋内部的负涡度向海岛靠拢的现象, 当把图4c中红框部分放大(图4f), 可以清楚看到在涡旋与海岛相切的南侧区域有涡度明显减小的现象。原反气旋式涡旋有部分则似乎从原涡旋中分离出来, 由海岛南侧绕过海岛, 形成一个反气旋式涡旋(图4c、d), 本研究称之为B涡旋。当把图4b中红框部分放大(图4e), 还可看出在涡旋与海岛碰撞的地方发生了等涡度线增密的现象, 并且由图4c、f可看出, 该处的等涡度线也沿着海岛发生了变形, 这在后面的讨论中有重要的意义。并且图5也显示, 其他深度也出现了同样的现象。基于涡旋碰撞过程中在垂直方向的相似反应, 下面将集中分析表层的结果。首先是为什么碰撞点的南北两侧区域会出现不一样的情况。为此, 本文将涡旋与海岛碰撞的区域划分为南北两个部分, 对南北两侧区域部分涡度方程各项的时间序列进行分析, 以此探讨出现上述现象的动力机制。
Fig.4 Surface (-1m) horizontal distribution of vorticity

图4 表层(z = -1m)涡度水平空间分布图

a: t=12d; b: t=17d; c: t=20d; d: t=28d。图中蓝、黄线箭头分别指示了B、C涡旋的大致位置; 海岛周围的“⊕”为碰撞区域的划分

Fig. 5 Horizontal distribution of vorticity at different depths on the 20th day of model integration

图5 t=20d时不同水深处的涡度水平空间分布图

a: 水深=100m; b: 水深=300m; c: 水深=500m; d: 水深=1000m

首先对碰撞区域进行区域划分, 如图6所示。涡旋的起始中心坐标为(812667m, 353833m), 起始半径为R0; 海岛在海表的半径为R1, 海岛中心点坐标为(560000m, 330000m)。将起始涡旋(黑色虚线圆)沿纬向平移至与海岛相切。连接海岛以及涡旋的中心作直线a, 并在海岛中心作该线的垂线b, 以海岛中心为圆心, 以涡旋与海岛相切时涡旋中心到海岛中心的距离R0+R1作为半径画圆(红色虚线圆), 该圆形区域与该垂线共同将海岛附近的区域划分为4个区域(蓝色填充区)。
Fig. 6 Regional division near the island

图6 海岛附近区域划分示意图

根据动量方程推导出的涡度方程是分析相对涡度局地变化的重要工具, 通过该公式可将不同物理因子导致的相对涡度的局地变化区分开来。涡度方程的垂直分量方程(Pedlosky, 1987)如下所示:
其中x、y和z是直角坐标系下的坐标, $\xi $为垂直涡度分量, t为时间, u、v、w分别为x、y、z方向上的速度, f为科氏参数, ρ为密度, p为压强。其中(Ⅰ)为涡度的局地时间变化项; (Ⅱ)为u速度涡度平流变化项; (Ⅲ)为v速度涡度平流变化项; (Ⅳ)为垂直平流变化项; (Ⅴ)为散度项; (Ⅵ)为斜压项; (Ⅶ)为扭转项。在本理想模型实验里, 水平黏性系数为零, 故摩擦效应项不包括在上述涡度方程里。
下面计算涡度方程中各项在区域①和区域④的平均, 计算结果见图7。根据涡度方程各项的比较分析, 可发现涡度的局地时间变化项的量级为10-10, 涡度方程中其他项(图7b—g)与局地时间变化项量级相当的有3项: u速度涡度平流项(图7b), v速度涡度平流项(图7c)和散度项(图7e), 其他项量级均较小, 故不予考虑, 这由图7h也可看出, 区域①的水平涡度平流项与散度项之和与涡度局地时间变化项几乎是重合的。
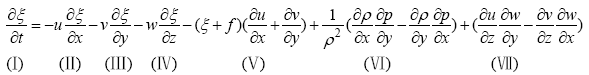
Fig. 7 Regionally averaged time series of different terms in the vorticity equation

图7 涡度方程各项区域平均的时间序列

蓝色实线为区域①; 红色实线为区域④。a. 局地变化项; b. u速度涡度平流变化项; c. v速度涡度平流变化项; d. 垂直平流变化项; e. 散度项; f. 斜压项; g. 扭转项; h. 区域①的水平涡度平流项+散度项和局地变化项的对比时间序列(蓝色实线: 水平涡度平流项+散度项; 绿色实线: 涡度局地时间变化项)。本文主要关注图中黑色虚线之间的时间段, 即涡旋碰撞海岛的时间段

图7只说明了u速度涡度平流项、v速度涡度平流项和散度项在涡旋碰撞海岛的过程中起主要作用, 那么这三项导致涡度增加的具体物理过程是怎样的呢?下面在碰撞南北两侧各取3个点, 分别分析这些点上的水平涡度平流项和散度项。
在分析之前, 首先对u速度涡度平流项和v速度涡度平流项的水平分布作一个简要说明。图8分别为u速度涡度平流项(图8a、c、e、g)和v速度涡度平流项(图8b、d、f、h)4个时次的水平分布图, 由这两幅图可看出, 涡旋外围u速度涡度平流项和v速度涡度平流项的分布分别有4个极值区域。本文用图9的示意图表示: 即将涡旋外围(注意这里的区域划分为涡旋外围的区域划分, 与前面图6的海岛周围区域划分不相同)划分为(Ⅰ)、(Ⅱ)、(Ⅲ)、(Ⅳ)区域, u速度涡度平流项的符号在外围按照(Ⅰ)、(Ⅱ)、(Ⅲ)、(Ⅳ)区域的顺序依次为-、+、-、+; v速度涡度平流项的符号在外围按照(Ⅰ)、(Ⅱ)、(Ⅲ)、(Ⅳ)区域的顺序依次为+、-、+、-。对比图8和图4, 可发现这4个极值区域大致为涡旋中图4a黑虚线圆框之间的区域, 这可由-u和x方向的涡度梯度在涡旋外围的符号分布分辨出来。根据涡度方程的定义, 这4个极值区域是涡旋结构中水平涡度平流项导致的涡度变化最剧烈的区域, 且由图4可看出C涡旋的生成是在此极值区域中产生, 且B涡旋的生成也和此极值区域有很大关系, 故后面探讨B涡旋、C涡旋的生成机制时主要关心的就是涡旋外围涡度平流项的极值区域。
为了研究涡旋外围涡度分布随时间的变化, 在碰撞点的北侧取黑、红、蓝3个点“×”, 如图8a、g所示, 分析这3个点的水平涡度平流项和散度项, 以及它们的拆分项。由图8a、g可看出, 当t=7d时蓝点“×”刚开始进入此极值区域, 当t=22d时黑点“×”刚离开此极值区域, 因此这里关注的时间段为t=7d到t=22d之间。需要注意的是黑点在涡旋与海岛作用的过程中几乎一直处于涡旋(Ⅱ)区域边缘处(C涡旋生成地), 而红、蓝两点则在涡旋靠近海岛时均穿过了(Ⅱ)区域。
Fig.8 Surface (-1m) distribution of the vorticity advection term in the x-direction(left) and y-direction(right)

图8 表层(z = -1m)u速度涡度平流项水平空间分布图(a. t=7d; c. t=13d; e. t=16d; g. t=22d)和v速度涡度平流项水平空间分布图(b. t=7d; d. t=13d; f. t=16d; h. t=23d)

a、g中的“×”与b、h中的“*”分别为分析涡度平流项和散度项随时间变化的位置

Fig. 9 Schematic of horizontal distribution of the vorticity advection terms in the periphery of the eddy

图9 u速度涡度平流项和v速度涡度平流项在涡旋外围的分布示意图

图10为这3点的水平涡度平流项和散度项的时间序列图。由图10可以看出, 黑点明显和其他两个点不同, 水平涡度平流项和散度项的量值均有明显增大, 由于蓝、红、黑点进入涡旋(Ⅱ)区域有时间上的先后顺序, 故该3点的图像会存在时间上的滞后变化。根据涡度方程, 黑点处u速度涡度平流项的增大将会导致该点处涡度的激增。通过该项的拆分项(图11a、b)可看出明显是由x方向的涡度梯度导致u速度涡度平流项的增大(图4b和4e可看到由于海岛的阻挡作用, 等涡度线发生了明显增密的现象)。并且由u速度涡度平流项的组成可看出, 该项和x方向的涡度梯度会出现正反馈的作用关系。同样, v速度涡度平流项(图10b)的量值也增大不少, 这同样也是涡度梯度导致的, 但由于该项为负, 故对黑点处气旋式涡旋的生成起相反作用。这里需要说明的是, 由于海岛的阻挡作用实际上也导致了$|-\mu|$和$\left| -v \right|$的增大。对于$\left| -v \right|$来说, 由图11c可明显看出; 对于$\left| -u \right|$来说, 由于前面已经说明了该3点的图像会存在时间上的滞后关系, 因此在关注图11a的相应曲线时, 对于蓝线也应该关注t=7d到t=22d时段的前面时段, 对于黑线则关注该时段的后面时段, 故由此可看出黑点的$\left| -u \right|$是有增大的。$\left| -u \right|$和$\left| -v \right|$的增大应该从角动量守恒定律及海岛对其附近背景流的阻挡作用来考虑。对于散度项(图10c)而言, 其量值的增大是由$-(\xi +f)$这部分导致的, 也就是涡度的增大导致的。故散度项的增大不是黑点处涡度增大的主导原因, 而是对黑点处涡度增大的响应。
Fig. 10 Time series of vorticity advection term in the x-direction(a) and y-direction(b), and the divergence term(c) to the right of the collision axis

图10 碰撞点北侧(沿移动方向碰撞点右侧)u速度涡度平流项(a)、v速度涡度平流项(b)、散度项(c)的时间序列图

黑色、红色、蓝色曲线分别代表图8a和图8g中黑、红、蓝三点

下面在碰撞点的南侧取黑、红、蓝三个点“*”, 如图8b和图8h所示, 进行同样的分析。同样, 由于当t=7d时蓝点“*”刚开始进入此极值区域, 当t=23d时黑点“*”刚离开此极值区域, 因此这里关注的时间段为t=7d到t=23d之间。
图12为这3点的水平涡度平流项和散度项的时间序列图, 可看出, 黑点也和其他两个点不同, 其中u速度涡度平流项(图12a)明显增大, 这同样是由x方向的涡度梯度导致的, 如图13a、b所示; 对于v速度涡度平流项(图12b)来说, 黑点处的符号竟然发生了变化, 前面介绍了该区域的v速度涡度平流项应该为正, 但这里竟然变为了负值。观察其拆分项(图13c、d), 这是由于y方向的涡度梯度的反向导致的。由图4f也可以看出此现象: 原本涡旋该处的y方向的涡度梯度为负, 但由于与海岛的作用反转为了正值。
Fig. 11 Time series of -u(a),$\frac{\partial \xi }{\partial x}$(b), -v(c),$\frac{\partial \xi }{\partial y}$(d),$-(\xi +f)$(e), and $(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y})$(f)

图11 -u (a)、$\frac{\partial \xi }{\partial x}$(b)、 -v(c)、$\frac{\partial \xi }{\partial y}$(d)、$-(\xi +f)$(e)、$(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y})$(f)的时间序列图

黑色、红色、蓝色曲线分别代表图8a和图8g中黑、红、蓝三点

对于散度项(图12c)而言, 该项为正, 对新的反气旋式涡旋的生成起负作用。由拆分项(图13e、f)可看出其量值的增大是由于$-(\xi +f)$和散度两部分共同导致的。从图13e可看出, 3点的$-(\xi +f)$量值以负值居多, 尤其是黑点, 几乎一直为负值, 且黑→红→蓝$-(\xi +f)$的绝对值依次递减。另外, 由$-(\xi +f)$可看出散度项受位置影响很大: 对比图13f和图11f, 可发现尽管均为碰撞点附近的格点, 但碰撞点南侧的散度在大部分时间均为负值, 说明碰撞点南侧均为下降流, 而碰撞点北侧的散度则呈正负震荡现象。因此, 该涡旋在与海岛碰撞后水体在垂向上主要从碰撞点南侧向下运动。所以散度项在B涡旋的生成过程中起缓冲作用, 减小了B涡旋的生成。
Fig. 12 Time series of vorticity advection term in the x-direction(a) and y-direction(b), and the divergence term(c) to the left of the collision axis

图12 海岛南侧(沿移动方向碰撞点之左侧)u速度涡度平流项(a)、v速度涡度平流项(b)和散度项(c)时间序列图

黑色、红色、蓝色曲线分别代表图8b和图8h中黑、红、蓝三点

Fig. 13 Time series of -u (a),$\frac{\partial \xi }{\partial x}$(b), -v (c),$\frac{\partial \xi }{\partial y}$(d),$-(\xi +f)$(e), and $(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y})$(f)

图13 -u(a)、$\frac{\partial \xi }{\partial x}$(b)、-v(c)、$\frac{\partial \xi }{\partial y}$(d)、$-(\xi +f)$(e)、$(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y})$(f)的时间序列图

黑色、红色、蓝色曲线分别代表图8b和图8h中黑、红、蓝三点

2.2 气旋式涡旋(北半球)

对于气旋式涡旋, 则刚好与反气旋式涡旋相反。如图14所示, 当气旋式涡旋以一定的速度碰撞一个尺度相当的海岛时(图14a), 气旋式涡旋的部分正涡度会从涡旋移动方向的右侧“绕”过海岛(图14b)形成一个气旋式涡旋(图14e)。同时, 在碰撞过程中, 会在移动方向碰撞点的左侧形成一个反气旋式涡旋(图14c、d、e)。
Fig.14 Surface(-1m) distribution of vorticity in the case of a cyclonic eddy colliding with an island

图14 表层(z = -1m)涡度水平空间分布图

a. t=10d; b. t=17d; c. t=20d; d. t=23d; e. t=28d

这里的分析类似于反气旋式涡旋, 由于反气旋式涡旋和气旋式涡旋的“-u”符号相反, 同样, “-v”、x方向上的涡度梯度和y方向上的涡度梯度符号均相反, 故气旋式涡旋和反气旋式涡旋的水平涡度平流项的分布结构是一致的, 即气旋式涡旋的u速度涡度平流项和v速度涡度平流项在涡旋外围的分布也如图9所示。因此当把图14c中红框部分放大(图14f), 可以清楚看到当气旋式涡旋与海岛发生碰撞时, 碰撞导致涡旋西侧等涡度线增密, 即x方向上的涡度梯度增大。由于(Ⅱ)区域u速度涡度平流项为正, (Ⅲ)区域u速度涡度平流项为负, 故(Ⅱ)区域的u速度涡度平流项会变大, (Ⅲ)区域的u速度涡度平流项会变小, 从而导致(Ⅱ)区域涡度的增大以及(Ⅲ)区域涡度的减小。其中(Ⅲ)区域涡度的减小就会导致该区域反气旋式涡旋的生成。对于v速度涡度平流项而言, 该项对于(Ⅲ)区域中反气旋式涡旋的生成影响不大, 这主要是由于在此案例中涡旋与海岛相撞主要是导致等涡度线在x方向增密, 而等涡度线在y方向的增密程度很小。对于(Ⅱ)区域来说, v速度涡度平流项会发生变号(同样是由于该区域y方向涡度梯度的反向), 使得(Ⅱ)区域v速度涡度平流项由“-”变为“+”; 再加上u速度涡度平流项在(Ⅱ)区域也增大了,因此(Ⅱ)区域的涡度会迅速增大, 导致原气旋式涡旋的部分涡度从海岛北侧“绕”过海岛形成一个新的气旋式涡旋。

3 对比文献中的类似实验

Cenedese(2002)做过气旋式涡旋与一个海岛作用的实验室实验, 根据其结果可知, 气旋式涡旋在碰到海岛后在海岛西北侧诱导出了一个气旋式涡旋, 这与本研究的实验是一致的, 但该文章没有关注是否有反气旋式涡旋的激发生成。
之后Cenedese等(2005)还做过气旋式涡旋与两个海岛作用的实验室实验, 结果表明气旋式涡旋的部分涡度均是从海岛的北侧“绕”过海岛(由涡旋本体和诱导涡旋的涡丝连接方向可看出)。另外, 该实验在北侧海岛的南侧诱导出了一个反气旋式涡旋, 这与本研究的结论均一致。
Andres等(2013) 做过涡旋与矩形障碍物碰撞的实验室实验, 结果发现, 反气旋式涡旋是从障碍物的南侧“绕”过障碍物, 气旋式涡旋是从障碍物的北侧“绕”过障碍物, 该障碍物的形状类似于一个矩形, 与本研究中的海岛形状不同, 但涡旋“绕”过圆形(本研究)与矩形障碍物的方向却是一致的。
此外, Herbette等(2003)利用数值实验研究了反气旋式涡旋与不露出海面的海山发生碰撞的过程, 并指出即使是不露出海面的海山, 反气旋式涡旋“绕”过海山的方向与本研究得出的结论也是一致的。
由此可知, 本研究得出的结论很可能是一个较为普适的结论, 但这还需要有更多的对比实验来进行验证。改变海岛的形状或大小、涡旋与海岛碰撞位置的变化、背景流强度的变化及涡旋强度的变化等, 都可能对结论产生影响。

4 结论与讨论

本研究利用ROMS模式进行了f-平面上涡旋碰撞海岛的理想模型实验。当北半球的反气旋式涡旋碰撞海岛时, 假设反气旋式涡旋移动的方向为x轴方向, 涡旋移动方向碰撞点右侧区域为(Ⅱ)区域, 涡旋移动方向碰撞点左侧区域为(Ⅲ)区域。由于海岛的阻挡作用将导致碰撞处的等涡度线的增密, 即x方向的涡度梯度的绝对值的增大, 而(Ⅱ)、(Ⅲ)区域的u速度符号是相反的, 从而导致涡旋外围u速度涡度平流项在(Ⅱ)区域的增大, 和(Ⅲ)区域的减小, 进而导致(Ⅱ)区域涡度的增大和(Ⅲ)区域的涡度减小。(Ⅱ)区域涡度的增大会导致该处气旋式涡旋的生成, (Ⅲ)区域涡度的减小则会导致反气旋式涡旋中的涡度在该处继续前行, 从而使该处的等涡度线沿着海岛的地形分布。对于v速度涡度平流项, 在碰撞过程中由于海岛的阻挡作用导致碰撞处(Ⅲ)区域的等涡度线沿着海岛的地形分布, 使得v速度涡度平流项在涡旋(Ⅲ)区域可能会发生变号, 由正变为负, 本实验中的碰撞情况即是如此, 从而导致(Ⅲ)区域涡度的进一步减小, 最终导致(Ⅲ)区域处原反气旋式涡旋的破裂, 最终诱导出反气旋式涡旋。由于该分析是在f-平面下进行的, 与纬度的变化不相关, 故可将实际中反气旋式涡旋以任何方向碰撞海岛的方向均视作x轴方向。
若海岛地形使得(Ⅲ)区域的v速度涡度平流项变为0左右, 即碰撞处海岛地形为类似Andres等(2013)实验中的矩形形状, 则涡度平流项可能导致(Ⅲ)区域处原反气旋式涡旋破裂速度小于本研究实验案例, 即可能导致诱导出的反气旋式涡旋小于本研究实验案例; 同理, 若海岛地形使得(Ⅲ)区域的v速度涡度平流项不发生变号, 例如将本研究中实验案例中的涡旋往北侧移动一些, 让碰撞点位于海岛的北部, 则原反气旋式涡旋很可能不发生破裂, 将不会诱导出新的反气旋式涡旋。
对散度项而言, 该项和位置有很大关系。对于本实验中的反气旋式涡旋, 其在气旋式涡旋的生成上由于主要受-(ξ+f)的变化控制, 故散度项对气旋式涡旋的生成不会起主导作用, 只起调节作用; 在反气旋式涡旋的生成中由于散度项和水平涡度平流项相比较小, 故也不对反气旋式涡旋的生成起主导作用, 而是起缓冲作用, 减小了反气旋式涡旋的生成, 从物理现象上可能表现为: 涡旋本体撞向海岛时, 一部分涡旋结构在水平上从海岛南侧“绕”过海岛, 还有一小部分涡旋水体在垂向上从海岛南侧向下运动。
通过上述讨论可看出, 海岛在涡旋与海岛碰撞过程中主要起阻挡作用, 该阻挡作用由两方面组成: 一是阻挡导致碰撞方向上的涡度梯度的绝对值的增加; 二是通过海岛地形的作用改变碰撞点附近等涡度线的形状。同时, 海岛还可能通过改变海岛附近的背景流的作用, 在碰撞前影响涡旋的移动路径, 从而减轻涡旋与海岛的碰撞作用。
对于北半球的气旋式涡旋, 由于气旋式涡旋和反气旋式涡旋的水平涡度平流项的分布结构一致, 故当其以一定的速度碰撞一个尺度相当的海岛时, 气旋式涡旋的部分涡度会从涡旋移动方向的右侧“绕”过海岛, 形成一个新的气旋式涡旋, 同时在碰撞过程中会在移动方向碰撞点的左侧形成一个反气旋式涡旋。上面的分析也显示, 碰撞过程中诱导出的新涡旋的具体位置和涡旋的旋转方向有关。因此对于南半球的反气旋式涡旋(逆时针旋转), 当其以一定速度碰撞一个尺度相当的海岛时, 反气旋式涡旋的部分涡度会从涡旋移动方向的右侧“绕”过海岛形成一个新的反气旋式涡旋; 同时在碰撞过程中会在移动方向碰撞点的左侧形成一个气旋式涡旋。对于南半球的气旋式涡旋(顺时针旋转)分析也类似。
从涡度方程的角度来看, 本研究阐述的海岛阻挡作用主要解释了水平涡度平流项在碰撞过程中的作用, 由于水平涡度平流项和纬度的变化无关, 也就是说该阻挡作用和科氏参数f或者β效应无关, 但其他项在碰撞过程中会有什么作用?会有哪些变化?本文阐述了海岛在水平上对涡旋的作用, 那在垂向上具体会有什么作用?这些都还需要进一步研究探讨。
应该看到, 本理想实验在设置上存在一些限制, 而且涡旋与海岛碰撞过程中受到诸多因素影响, 比如海岛的形状、大小, 涡旋与海岛碰撞位置的变化, 背景流强度的变化, 涡旋强度的变化等。这些在本文中未予讨论的问题, 也是我们目前正在进行的工作内容。

The authors have declared that no competing interests exist.

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
陈更新, 2010. 南海中尺度涡的时空特征研究[D]. 青岛: 中国科学院研究生院(海洋研究所): 1-120.

CHEN GENGXIN, 2010. Mesoscale eddies in the South China Sea: mean properties and spatio-temporal variability[D]. Qingdao: The Institute of Oceanology, Chinese Academy of Sciences: 1-120 (in Chinese with English abstract).

[2]
管秉贤, 袁耀初, 2006. 中国近海及其附近海域若干涡旋研究综述Ⅰ. 南海和台湾以东海域[J]. 海洋学报, 28(3): 1-16.

GUAN BINGXIAN, YUAN YAOCHU, 2006. Overview of studies on some eddies in the China seas and their adjacent seas Ⅰ. The South China Sea and the region east of Taiwan[J]. Acta Oceanologica Sinica, 28(3): 1-16 (in Chinese with English abstract).

[3]
林鹏飞, 王凡, 陈永利, 等, 2007. 南海中尺度涡的时空变化规律Ⅰ. 统计特征分析[J]. 海洋学报, 29(3): 14-22.

LIN PENGFEI, WANG FAN, CHEN YONGLI, et al, 2007. Temporal and spatial variation characteristics on eddies in the South China Sea Ⅰ. Statistical analyses[J]. Acta Oceanologica Sinica, 29(3): 14-22 (in Chinese with English abstract).

[4]
王东晓, 1996. 南海表层水温年循环与年际变化的研究[D]. 青岛: 中国海洋大学: 1-154.

WANG DONGXIAO, 1996. The annual cycle and the interannual variability of sea surface temperature in the South China Sea[D]. Qingdao: Institute of Oceanology, Chinese Academy of Sciences: 1-154 (in Chinese with English abstract).

[5]
ADDUCE C, CENEDESE C, 2004. An experimental study of a mesoscale vortex colliding with topography of varying geometry in a rotating fluid[J]. Journal of Marine Research, 62(5): 611-638.

[6]
ANDRES M, CENEDESE C, 2013. Laboratory experiments and observations of cyclonic and anticyclonic eddies impinging on an island[J]. Journal of Geophysical Research: Oceans, 118(2): 762-773.

[7]
ARHAN M, MERCIER H, LUTJEHARMS J R E, 1999. The disparate evolution of three Agulhas rings in the South Atlantic Ocean[J]. Journal of Geophysical Research: Oceans, 104(C9): 20987-21005.

[8]
CALIL P H R, RICHARDS K J, JIA YANLI, et al, 2008. Eddy activity in the lee of the Hawaiian Islands[J]. Deep Sea Research Part Ⅱ: Topical Studies in Oceanography, 55(10-13): 1179-1194.

[9]
CENEDESE C, 2002. Laboratory experiments on mesoscale vortices colliding with a seamount[J]. Journal of Geophysical Research: Oceans, 107(C6): 6-1-6-14.

[10]
CENEDESE C, ADDUCE C, FRATANTONI D M, 2005. Laboratory experiments on mesoscale vortices interacting with two islands[J]. Journal of Geophysical Research: Oceans, 110(C9): C09023.

[11]
CHELTON D B, SCHLAX M G, SAMELSON R M, 2011. Global observations of nonlinear mesoscale eddies[J]. Progress in Oceanography, 91(2): 167-216.

[12]
CHEN GENGXIN, GAN JIANPING, XIE QIANG, et al, 2012. Eddy heat and salt transports in the South China Sea and their seasonal modulations[J]. Journal of Geophysical Research: Oceans, 117(C5): C05021.

[13]
CHEN GENGXIN, XUE HUIJIE, 2014. Westward intensification in marginal seas[J]. Ocean Dynamics, 64(3): 337-345.

[14]
CHENG XUHUA, QI YIQUAN, 2010. Variations of eddy kinetic energy in the South China Sea[J]. Journal of Oceanography, 66(1): 85-94.

[15]
CHOW C H, HU J H, CENTURIONI L R, et al, 2008. Mesoscale Dongsha cyclonic eddy in the northern South China Sea by drifter and satellite observations[J]. Journal of Geophysical Research: Oceans, 113(C4): C04018.

[16]
HERBETTE S, MOREL Y, ARHAN M, 2003. Erosion of a surface vortex by a seamount[J]. Journal of Physical Oceanography, 33(8): 1664-1679.

[17]
MCWILLIAMS J C, FLIERL G R, 1979. On the evolution of isolated, nonlinear vortices[J]. Journal of Physical Oceanography, 9(6): 1155-1182.

[18]
NOF D, 1983. The translation of isolated cold eddies on a sloping bottom[J]. Deep Sea Research Part A. Oceanographic Research Papers, 30(2): 171-182.

[19]
PEDLOSKY J, 1987. Geophysical fluid dynamics[M]. 2nd ed. New York: Springer-Verlag: 35-38.

[20]
ROBINSON A R, 1983. Eddies in marine science[M]. Berlin Heidelberg: Springer-Verlag: 1-5.

[21]
SCHOUTEN M W, DE RUIJTER W P M, VAN LEEUWEN P J, et al, 2000. Translation, decay and splitting of Agulhas rings in the southeastern Atlantic Ocean[J]. Journal of Geophysical Research: Oceans, 105(C9): 21913-21925.

[22]
SIMMONS H L, NOF D, 2000. Islands as eddy splitters[J]. Journal of Marine Research, 58(6): 919-956.

[23]
SMITH D C, O'BRIEN J J, 1983. The interaction of a two-layer isolated mesoscale eddy with bottom topography[J]. Journal of Physical Oceanography, 13(9): 1681-1697.

[24]
THIERRY V, MOREL Y, 1999. Influence of a strong bottom slope on the evolution of a surface-intensified vortex[J]. Journal of Physical Oceanography, 29(5): 911-924.

[25]
VAN GEFFEN J H G M, DAVIES P A, 2000. A monopolar vortex encounters an isolated topographic feature on a β-plane[J]. Dynamics of Atmospheres and Oceans, 32(1): 1-26.

[26]
WANG GUOHUI, DEWAR W K, 2003a. Meddy-seamount interactions: Implications for the Mediterranean salt tongue[J]. Journal of Physical Oceanography, 33(11): 2446-2461.

[27]
WANG GUIHUA, SU JILAN, CHU P C, 2003b. Mesoscale eddies in the South China Sea observed with altimeter data[J]. Geophysical Research Letters, 30(21): 2121.

[28]
WILLIAMS S, HECHT M, PETERSEN M, et al, 2011. Visualization and analysis of eddies in a global ocean simulation[J]. Computer Graphics Forum, 30(3): 991-1000.

[29]
XIU PENG, CHAI FEI, SHI LEI, et al, 2010. A census of eddy activities in the South China Sea during 1993-2007[J]. Journal of Geophysical Research: Oceans, 115(C3): C03012.

[30]
ZHANG ZHENGGUANG, WANG WEI, QIU BO, 2014. Oceanic mass transport by mesoscale eddies[J]. Science, 345(6194): 322-324.

[31]
ZHANG ZHENGGUANG, ZHANG YU, WANG WEI, et al, 2013. Universal structure of mesoscale eddies in the ocean[J]. Geophysical Research Letters, 40(14): 3677-3681.

Options
文章导航

/

〈 〉