Search
E-mail
RSS

Online submission Editor-in-chief Peer review Staff Login

Journal of Tropical Oceanography >

2017 , Vol. 36 >Issue 3: 86 - 93

DOI: https://doi.org/10.11978/2016082

Orginal Article

Seismic illumination analysis based on the Poynting vector

  • PANG Xinming , 1, 3 ,
  • ZHAO Minghui , 1 ,
  • ZHANG Min 2 ,
  • YANG Guoquan 2
Expand
  • 1. CAS Key Laboratory of Ocean and Marginal Sea Geology, South China Sea Institute of Oceanology, Guangzhou 510301, China
  • 2. School of Geosciences of China University of Petroleum (East China), Qingdao 266580, China
  • 3. Graduate University of Chinese Academy of Sciences, Beijing 100049, China;
Corresponding author: ZHAO Minghui. E-mail:

Received date: 2016-09-02

  Request revised date: 2016-10-10

  Online published: 2017-06-01

Supported by

Natural Science Foundation of China (91428204, 41376063, 41176053)

Copyright

热带海洋学报编辑部
Fold

Abstract

Research on seismic wave field decomposition and Gaussian de-noising and directional illumination in three- dimensional (3D) models will promote a wide application of seismic illumination based on the Poynting vector. In this paper, optimal angle illumination is found through obtaining the acquisition parameter by laying source in the target area, namely reversed illumination, then decomposing the wave field transmitting from best source position based on the Poynting vector, and using statistics on the energy of different angles. In addition, the de-noised wave filed obtained by Gaussian filter improves the stability and fidelity of wave field decomposition, which demonstrates the effectiveness of the method. Compared to the traditional ray-tracing illumination, illumination based on double way wave equation avoids high frequency approximation, whose information of wave field is more comprehensive compared with one-way wave equation and whose calculation is more efficient. With weighted de-noising, the fidelity and signal-to-noise ratio of the wave field are improved. Moreover, the method is developed in the 3D model to realize dip illumination and azimuth illumination. These results not only provide scientific basis for seismic observation system of complex 2D geological model, but also offer a base for future applications in optimization of 3D acquisition parameters, which is advantageous to promote applied domain of the Poynting vector.

Key words： seismic illumination; Poynting vector; Gaussian weighted method; directional decomposition

Cite this article

PANG Xinming , ZHAO Minghui , ZHANG Min , YANG Guoquan . Seismic illumination analysis based on the Poynting vector[J]. Journal of Tropical Oceanography, 2017 , 36(3) : 86 -93 . DOI: 10.11978/2016082

照明分析在地震采集、处理和成像过程中是非常有价值的质控手段, 特别是当研究目标区域存在高陡构造、斜坡和异常体等特征时, 照明分析显得尤为重要。地震照明手段主要有两方面应用: 一是在数据采集前对观测系统评估和优化, 节省经济成本(吕公河 等, 2006; 秦广胜 等, 2010; 温书亮 等, 2011; 朱金平 等, 2011); 二是分析由于不均匀照明引起的成像阴影区域, 修改偏移成像条件进行照明补偿。其中, 求取照明的强度和角度是计算的重点, 为了计算内存和精度符合计算机和现场作业的要求, 需要运用合适的波场传播方程和波场角度分解方法。
地震照明分析是基于正演模拟展开的, 主要包括射线追踪方法和波动方程方法。射线追踪可以快速提供波场传播方向信息(Lecomte et al, 1998), 但因为本身高频近似的限制不可避免存在误差。波动方程方法包括单程波和双程波: 单程波方程(Wu et al, 2006; Xie et al, 2006； 杨敬磊 等, 2008)相比于射线追踪, 精度提高, 除了提供地震传播方向信息, 还可以对偏移成像进行照明补偿(Wu et al, 2002; Jin et al, 2003; Rickett, 2003; 陈生昌 等, 2007), 但是单程波算子本身对大方位角度的波场计算存在限制, 而且对每个质点的格林函数进行角度域分解需要大量的时间和空间内存, 这时采用平面波照明分析(Liu et al, 2002; 冯伟 等, 2004; Liu et al, 2005; 孙伟家 等, 2007、2011)可以兼顾计算效率与精度; 相比较单程波方程, 基于双程波方程的照明分析不仅涵盖了宽方位角度信息, 而且反映的是全波信息(董良国 等, 2006; 李万万, 2008; Xie et al, 2008; 徐峰 等, 2012)。裴正林(2008)基于双程波声波方程利用坡印亭矢量进行波场方向性分解, 计算定向照明度, 提供了一种计算精度高、计算速度快的方法; 雷涛等(2014)不仅考虑直达波还包括反射波, 基于声波方程考虑整个时间尺度上不同方向的波场值, 从而进行能量叠加, 基于坡印廷的矢量计算目标区域照明度, 为观测系统评价提供量化信息。除此之外, 逆时偏移成像条件里引入坡印亭矢量算子, 在正传波场和反传波场互相关时提供角度限制条件, 提高了角道集的成像质量(Yoon et al, 2011)。
为了避免大量计算和角度限制, 本文首先采用双程波声波方程基于坡印亭矢量针对地下目标进行波场分解, 并且将反向照明和坡印廷矢量联合使用, 得到面向目标区域的最优的采集参数设置; 其次, 针对坡印廷矢量本身的求导算法容易产生噪音, 采用高斯函数加权去噪(Yoon et al, 2011), 并且详细讨论加权函数对去噪效果的影响, 对计算结果的稳定性和保真度进行分析; 最后, 基于上述定向照明度的二维计算, 将其扩展到三维模型, 研究该方法在地球物理中的广泛适用性。

1 方法原理

在已知速度模型和观测系统的前提下, 照明度用来描述地震波在地下传播时的能量分布。双程波算子是最为准确的表达直达波、反射波和透射波等能量传播的运算(李万万, 2008), 文中采用交错网格有限差分方法求解双程波声波波动方程, 并采用完全匹配层边界条件, 从而得到每一个时刻的波场值。照明度与正演模拟的结果不同, 得到的结果不考虑模型反射系数, 反映的是观测系统分布情况对速度模型的能量分布也就是振幅分布的均衡程度。所以, 单一炮点单一检波点单一时刻对应的某一空间点的照明度表示为公式(1):
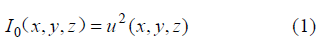
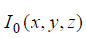式中: 表示空间点(x, y, z)的照明度(单位: W•m-2); 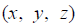表示波场在空间点(x, y, z)的振幅值(单位: N•m-2)。考虑整体观测系统对地下模型的总照明度如公式(2):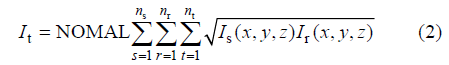
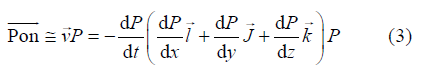
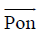式中: It表示整个速度模型的照明度; Is表示单一炮点在空间点(x, y, z)的照明度; Ir表示单一检波点在空间点(x, y, z)的照明度; ns表示震源的数目; nr表示检波器的数目; nt表示波场传播的时间除以时间采样间隔得到的数目; NOMAL表示归一化算子。
在时间域里波场方向信息不明显, 文中基于坡印亭矢量方法提取波场定向方向信息。声波能流密度用坡印亭矢量可以表示为公式(3)(Yoon et al, 2006):
式中: 为坡印亭矢量(单位: W•m-1); 为速度矢量(单位: m•s-1); P{Invalid MML}为声波应力(单位:N); 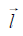为x轴正方向的单位矢量; 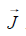为y轴正方向的单位向量; 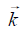为z轴正方向的单位向量。
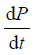在时间域里采用交错网格有限差分求取声波应力值P, 以及该应力的一阶时间导数 和空间导数 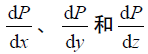, 代入公式(3)得到坡印廷矢量 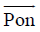, 坡印廷矢量的方向表征地震波能量传播的方向, 也就是照明方向。在二维情况下, 用坡印廷矢量与垂直方向的夹角作为照明的传播方向; 在三维情况下, 坡印廷矢量的方向与垂直方向为倾角, 坡印廷矢量在水平面的投影与水平方向的夹角作为方位角, 由此得到了表征照明的方向。由公式(2)和(3)分别得到了照明能量的强度和方向。
在计算坡印亭矢量值时, 当子波为最大值时, 导数对应的是零值, 经过一段时间后, 导数绝对值达到最大值, 所以, 采用高斯加权函数, 如公式(4)所示, 对每一个点的值均取周围函数的加权值, 加强了稳定性, 控制了随机噪音的产生(Yoon et al, 2011)。
式中: w表示高斯权重分布值, 在照明加权中用w乘以时窗内波形内的每一值; μ表示坡印廷矢量随机分布中的均值, 在照明加权中取加权时窗的中心位置值; σ表示坡印廷矢量随机分布中的标准差, 在照明加权中取值可试算, 影响不大; x表示加权时窗内的任一点位置。
波场的方向性分解实现了地下模型的角度照明。针对地下目标体, 通过角度照明可以得到观测系统参数设计对目标体有利信息的贡献度, 因为在全波形反演或者逆时偏移成像中, 不是所有的数据信息都是必要的或者是有利用价值的, 可能信噪比高、同相轴连续的优质炮记录在成像中因为全波信息的引入会产生干扰, 比如噪音、假象或者低分辨率。对于特定倾角的地下目标体, 不同角度的炮检组合对实际成像有不同的照明贡献值, 因此, 可以设置权值使观测系统参数对地下目标体能量的贡献达到最大化, 这时照明度就作为一个标尺, 通过得到的角度信息进行炮记录筛选以及成像条件的改变。

2 数值试验

2.1 盐丘模型试算

图1是盐丘模型, 速度模型的横纵向间隔均是4m, 面积是5.16km×1.2km, 中间部分是高陡异常体构造, 尖锐凸起延伸到近地表结构中。高速体结构对波场传播影响很大, 适用于照明方向的研究工作。其中红色椭圆框中的区域是目标区, 也是在成像中由于采集算子和偏移算子的限制容易出现阴影的区域。
Fig. 1 The salt dome model. The red circle is the target area

图1 盐丘模型, 红色圆为目标区

在目标区域设置震源, 在地面均匀放置检波器, 基于双程波波动方程得到目标区域的反向照明图(图2a), 可以看到, 由于高速遮挡, 大部分能量全反射折回到模型的右下方, 只有少部分能量到达地面, 提取图2a中红线位置的能量做归一化后如图2b所示, 主要集中在2km到4km之间。根据互换原理, 主要研究地面2km到4km之间的炮点分布以及角度定向照明度对目标区域的影响。
Fig. 2 Reversed illumination of the target area. (a) The energy distribution about reversed illumination; (b) surface energy distribution of reversed illumination (corresponding to the red line in Fig. 2a)

图2 目标区域反向照明图^a. 反向照明能量图, 图中红线表示地表位置; b. 地表能量分布图, 对应图a中红线部分

图2b显示3.33km处反向照明的能量最强, 在该处放炮, 所有检波器置于地下4m处, 采用全接收方式, 3.33km处单炮的能量在穿过异常体后, 大部分集中在目标区域, 贡献了大部分照明度(图3a)。基于坡印廷矢量定向分解波场能量, 分析不同方向的照明度对目标区域的贡献。如图3b所示, 根据坡印廷矢量分解图3a所示的目标区域内不同方向传播的能量分布, 可以看到垂直向下传播的能量对目标区域贡献的最多, 这也不难理解, 震源位置几乎在目标区域的正上方, 除此之外, 45°到65°贡献了其余的能量值。
Fig. 3 Illumination of different directions in the target area when placing the source at 3.33 km. (a) Normalized energy distribution; (b) quantized energy distribution of different directions in the target area based on the Poynting vector (corresponding to Fig. 3a)

图3 在3.33km处放置震源时目标区域不同照明方向的照明图^a. 归一化能量分布图; b. 基于坡印廷矢量分解的不同方向的能量分布

通过反向照明得到地面最佳放置观测系统的范围是2km到4km; 从反向照明的结果中找到最大贡献值的位置; 分析该处的定向照明度对目标区域的贡献, 得到0°、45°~65°对于目标区域是最佳入射角度。这种思路对平面波偏移处理, 逆时偏移成像条件的设置都有参考价值。
为了验证上述结果, 图4a和图4b设置相同的观测系统, 在纵向深度2~4km处放置200炮, 分别得到总的地下照明度(图4a), 和震源作为组合形式以45°~65°入射角对模型进行照明分析, 得到照明能量分布图(图4b), 再次验证了不同角度的照明值对平面波逆时偏移的角度选择有着参考意义。
Fig. 4 Illumination energy from 2 km to 4 km of salt dome model. (a) Total illumination energy of 200 sources; (b) illumination energy when the plane angle is changed from 45 to 65

图4 盐丘模型2km到4km的照明能量图^a. 200炮的总照明度; b. 平面波45°到65°时照明能量分布图

从图4a和图4b中分别抽取目标区域的照明能量值进行对比, 在目标区内, 同样的炮数, 入射角度优化后大大提高了照明能量的贡献值(图5)。因为速度模型本身高速异常的隆起, 使得目标区处的能量相对很弱, 通过改变入射角度相对程度地提高提高了目标区的能量, 说明该方法是可行且有效的。
Fig. 5 Comparison of percentage of illumination energy in the target area before and after angle optimization. The dash line and solid line correspond to the illumination energy in Fig. 4a and Fig. 4b, respectively

图5 入射角度优化前后目标区域照明能量对比图^虚线与实线分别对应图4a和图4b中的照明能量

2.2 去噪模型试算

前面通过反向照明和定向照明联合确定了采集参数取值, 并且将结果应用到平面波的射线参数设置中。坡印廷矢量没有广泛地应用在双程波中, 主要是因为其计算方法本身容易产生噪音, 影响计算结果, 现在采用高斯加权函数对坡印廷矢量进行去噪。加入高斯加权函数的目的是加强算法的稳定性, 为了去除速度结构对结果的影响, 采用均匀模型介质; 为了去除观测系统参数对结果的影响, 采用单炮照明。图6展示了加入高斯加权系数前后, 单炮照明能量、水平分量、垂直分量、定向分解波场后的波场快照的对比情况。图6b明显去除了图6a左上角的噪音干扰; 图6c和图6d、图6e和图6f分别是水平分量和垂直分量在进行高斯加权前后的对比图; 图6g和图6h是对均匀模型传播的波场进行角度分解, 因为在均匀模型中, 没有其他干扰因素, 在任一角度上的波场分布都因为坡印廷矢量算子本身与导数计算所带来噪音, 充分体现了加入高斯加权系数后对于去噪的有效性。
Fig. 6 Comparison of results before and after adding Gaussian weight. (a) and (b) show one source illuminations from 30 to 60 (the black rectangular shows the noise); (c) and (d) show horizontal component; (e) and (f) show vertical component; (g) and (h) show wave snapshots extracted from 30 to 60 angles, before and after adding Gaussian weight, respectively

图6 高斯加权前后的对比图^a和b分别是应用高斯加权前后的30°~60°的单炮照明图(图中黑色矩形框内是噪音干扰); c和d分别是应用高斯加权前后的水平分量; e和f分别是应用高斯加权前后的垂直分量; g和h分别是应用高斯加权前后30°~60°的波场快照图

为了分析波场定向分解后波形是否产生畸变, 分别从完整的波场快照、定向分解30°到60°的波场快照和加入高斯加权之后的30°到60°的波场快照中, 抽取不同传播方向的波形进行对比(图7)。图7中显示了30°、35°、45°和60°的波场在某一时刻的波形对比, 其中, 红色线段代表从完整的波场分布中抽取的波形, 蓝色线段代表从定向分解的30°到60°的角度波场中抽取的波形, 橄榄绿线段代表从加入高斯权重的定向分解的30°到60°波场中抽取的波形。可以看出, 除了30°的波形, 其他角度的波形在加入加权系数后, 和波场快照的重合度提高很多, 噪音影响降低, 特别是45°的波形对比, 坡印廷矢量提取的波形值和完整的波场快照中提取的波形完全重合, 证明了这种方法对计算结果提高了保真度。
Fig. 7 Comparison of three kinds of waveforms among different transmitting angles, in which the red line represents the waveform extracted from a complete wave snapshot; a blue line represents the waveform extracted from directional composition wave field between 30 and 60; and an olive green line represents the waveform added Gaussian weight based on the blue line. (a), (b), (c), and (d) are waveform comparison when angle=60, angle=45, angle=35, and angle=30, respectively

图7 不同传播角度的3种波形对比^a. 60°时的波形对比; b. 45°时的波形对比; c. 35°时的波形对比; d. 30°时的波形对比。红色线段代表从完整的波场分布中抽取的波形; 蓝色线段代表从定向分解的30°到60°的角度波场中抽取的波形; 橄榄绿色线段代表从加入高斯权重的30°到60°定向分解的波场中抽取的波形

2.3 三维层状模型试算

图8a是三维层状速度模型的单炮照明能量图, 模型长宽高分别是810m、810m和510m, 由上至下分为3层, 速度分别设定为2000m•s-1、3000m•s-1和4000m•s-1。震源位于水平面中心位置(图8a中黑色五角星所示), 得到的照明度能量分布是以震源为中心对称的, 前面和右面分别是x轴255m位置对应的切面以及y轴55m位置对应的切面。可以看到切面的照明度分布和二维情况是一致的, 从浅到深能量逐渐减小。前切面位置处于中心震源处, 地震波能量穿过第一层界面, 有透射能量, 也有反射能量, 较少能量到达第三层; 右切面剖面离中心震源稍远, 能量大部分仍在第一层内。
Fig. 8 Directional illumination based on the three- horizontal-layer model. (a) one source illumination when the black star represents the seismic source; (b) directional illumination of one source when the azimuth angle is fixed; (c) directional illumination of one source when the dip angle is fixed

图8 三层水平层状模型方向照明图^a. 单炮照明图, 黑色五角星是震源的位置; b. 方位角固定的单炮照明图; c. 倾角固定的单炮照明图

在二维坡印亭矢量中加入y轴分量, 实现三维定向照明。在三维单炮照明度(图8a)的基础上, 固定倾角在30°到70°时, 得到方位角的照明范围(图8b), 图8b中显示的是穿过中心震源的切面。固定方位角的角度, 得到倾角的照明范围(图8c), 顶面显示的是方位角的范围, 前切面和右切面显示的能量分布, 均符合能量分布规律。因此, 坡印亭矢量方法在三维宽方位角采集成像中可以有效应用于地下目标体的照明分析。

2.4 三维盐丘模型试算

为了证明方法对三维复杂地质体的适用性, 截取SEG三维盐丘模型的一部分作为研究对象, 模型长宽高分别为600m、600m和500m (图9), 模型前面和右面显示的是三维盐丘中心切面, 出露的高速侵入体速度最大为4482m•s-1。图10a显示的是单炮照明能量图, 震源位于水平面中心位置(图10a中黑色五角星), 得到的照明度能量分布和理论上地震波的传播分布一致, 前面与右面分别是x轴100m位置对应的切面以及y轴300m位置对应的切面。可以看到切面的照明度分布和二维情况是一致的, 大部分能量遇到高速体后, 被反射到浅层(图10a)。基于三维坡印廷矢量进行方位角照明和倾角照明(图10b和图10c)均得到很好效果。复杂模型的适用也印证方法的可行性。
Fig. 9 Three-dimensional velocity model of a salt dome

图9 三维盐丘速度模型

Fig. 10 Three-dimensional directional illumination of a salt dome. (a) One source illumination based on the three- dimensional model of a salt dome. The black star represents one seismic source; (b) Directional illumination of one source when the azimuth angle is fixed; (c) Directional illumination of one source when the dip angle is fixed

图10 三维盐丘方向照明^a. 盐丘模型的单炮照明图, 黑色五角星是震源的位置; b. 方位角固定的单炮照明图; c. 倾角固定的单炮照明图

3 结论

通过上述讨论分析, 得到以下结论:
1) 基于双程波声波波动方程, 利用坡印亭矢量定向分解波场, 针对目标区, 利用反向照明得到目标区的有利震源分布范围, 根据最佳震源分布点的坡印廷矢量照明度, 获得了最佳定向照明角度, 以此实现了定向照明, 优化了观测系统与采集参数, 有利于平面波偏移等应用。
2) 利用高斯加权实现坡印廷矢量去噪, 通过波场快照与波形对比, 证明这种方法提高了分辨率与保真度, 展现了坡印廷矢量的广泛应用前景。
3) 基于三维层状介质模型利用坡印廷矢量, 实现了定向倾角照明与方位角照明, 证明了这种方法在三维采集设计中的可行性, 并且通过三维盐丘模型的试算, 证明了该方法对复杂模型的适用性, 可以为三维采集成像设计提供依据。

The authors have declared that no competing interests exist.

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
陈生昌, 马在田, 吴如山, 2007. 波动方程双程地下方向照明分析[J]. 同济大学学报(自然科学版), 35(5): 681-684, 704.

CHEN SHENGCHANG, MA ZAITIAN, WU RUSHAN, 2007. Two-way subsurface directional illumination analysis by wave equation[J]. Journal of Tongji University (Natural Science), 35(5): 681-684, 704 (in Chinese).

[2]
董良国, 吴晓丰, 唐海忠, 等, 2006. 逆掩推覆构造的地震波照明与观测系统优化[J]. 石油物探, 45(1): 40-47.

DONG LIANGGUO, WU XIAOFENG, TANG HAIZHONG, et al, 2006. Seismic wave illumination for overthrust nappe structures and optimal seismic survey design[J]. Geophysical Prospecting for Petroleum, 45(1): 40-47 (in Chinese).

[3]
冯伟, 王华忠, 吴如山, 等, 2004. 面向目标控制照明的合成波源偏移[J]. 石油物探, 43(3): 223-228.

FENG WEI, WANG HUAZHONG, WU RUSHAN, et al, 2004. The migration of synthetic waves for target-oriented controlled illumination[J]. Geophysical Prospecting for Petroleum, 43(3): 223-228 (in Chinese).

[4]
雷涛, 顾汉明, 李列, 等, 2014. 面向目标靶区的双程波动方程地震定向照明分析[J]. 石油物探, 53(4): 437-443.

LEI TAO, GU HANMING, LI LIE, et al, 2014. Target-oriented seismic directional illumination analysis based on two-way acoustic wave equation[J]. Geophysical Prospecting for Petroleum, 53(4): 437-443 (in Chinese).

[5]
李万万, 2008. 基于波动方程正演的地震观测系统设计[J]. 石油地球物理勘探, 43(2): 134-141.

LI WANWAN, 2008. Design of seismic geometry based on wave equation forward simulation[J]. Oil Geophysical Prospecting, 43(2): 134-141 (in Chinese).

[6]
吕公河, 尹成, 周星合, 等, 2006. 基于采集目标的地震照明度的精确模拟[J]. 石油地球物理勘探, 41(3): 258-261.

LYU GONGHE, YIN CHENG, ZHOU XINGHE, et al, 2006. Precious simulation of seismic illumination based on acquired targets[J]. Oil Geophysical Prospecting, 41(3): 258-261 (in Chinese).

[7]
裴正林, 2008. 波动方程地震定向照明分析[J]. 石油地球物理勘探, 43(6): 645-651.

PEI ZHENGLIN, 2008. Analysis on wave equation seismic directional illumination[J]. Oil Geophysical Prospecting, 43(6): 645-651 (in Chinese).

[8]
秦广胜, 蔡其新, 汪功怀, 等, 2010. 基于叠前成像的三维地震观测系统设计[J]. 地球物理学进展, 25(1): 238-248.

QIN GUANGSHENG, CAI QIXIN, WANG GONGHUAI, et al, 2010. 3D seismic geometry design based on pre-stack imaging[J]. Progress in Geophysics, 25(1): 238-248 (in Chinese).

[9]
孙伟家, 符力耘, 碗学检, 2007. 基于相位编码的地震照明度分析[J]. 石油地球物理勘探, 42(5): 539-543.

SUN JIAWEI, FU LIYUN, WAN XUEJIAN, 2007. Phase encoding-based seismic illumination analysis[J]. Oil Geophysical Prospecting, 42(5): 539-543 (in Chinese).

[10]
孙伟家, 符力耘, 胡善政, 等, 2011. 基于相位编码的Fourier变换波动方程三维地震照明分析[J]. 地球物理学进展, 26(4): 1249-1257.

SUN WEIJIA, FU LIYUN, HU SHANZHENG, et al, 2011. 3D Fourier transform wave-equation-based seismic illumination analysis with phase encoding[J]. Progress in Geophysics, 26(4): 1249-1257 (in Chinese).

[11]
温书亮, 尹成, 李绪宣, 等, 2011. 地震照明分析技术在深海地震数据采集设计中的应用[J]. 石油地球物理勘探, 46(4): 506-512.

WEN SHULIANG, YIN CHENG, LI XUXUANG, et al, 2011. Seismic illumination method and its application in seismic geometry design in deep waters[J]. Oil Geophysical Prospecting, 46(4): 506-512 (in Chinese).

[12]
徐峰, 陈立, 苏悦, 等, 2012. 基于目的层反射能量二次导数的炮检距设计[J]. 西南石油大学学报(自然科学版), 34(2): 72-78.

XU FENG, CHEN LI, SU YUE, et al, 2012. An offset design based on second derivative of target stratum energy[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 34(2): 72-78 (in Chinese).

[13]
杨敬磊, 李振春, 叶月明, 等, 2008. 地震照明叠前深度偏移方法综述[J]. 地球物理学进展, 23(1): 146-152.

YANG JINGLEI, LI ZHENCHUN, YE YUEMING, et al, 2008. Review of seismic illumination pre-stack depth migration methods[J]. Progress in Geophysics, 23(1): 146-152 (in Chinese).

[14]
朱金平, 董良国, 程玖兵, 2011. 基于地震照明、面向勘探目标的三维观测系统优化设计[J]. 石油地球物理勘探, 46(3): 339-348.

ZHU JINPING, DONG LIANGGUO, CHENG JIUBING, 2011. Target-oriented 3D seismic optimal geometry design based on seismic illumination[J]. Oil Geophysical Prospecting, 46(3): 339-348 (in Chinese).

[15]
JIN SHENGWEN, WALRAVEN D, 2003. Wave equation GSP prestack depth migration and illumination[J]. The Leading Edge, 22(7): 606-610.

[16]
LECOMTE I, GELIUS L J, 1998. Have a look at the resolution of prestack depth migration for any model, survey and wavefields[C]. New Orleans: SEG Technical Program Expanded Abstracts: 1112-1115.

[17]
LIU FAQI, STOLT R H, HANSON D W, et al, 2002. Plane wave source composition: an accurate phase encoding scheme for prestack migration[C]. Salt Lake City: SEG Technical Program Expanded Abstracts: 1156-1159.

[18]
LIU SHOUWEI, GENG JIANHUA, FENG WEI, 2005. Controlled illumination and seismic acquisition geometry for target-oriented imaging[J]. Applied Geophysics, 2(4): 230-234.

[19]
RICKETT J E, 2003. Illumination-based normalization for wave-equation depth migration[J]. Geophysics, 68(4): 1371-1379.

[20]
WU RUSHAN, CHEN LING, 2002. Mapping directional illumination and acquisition-aperture efficacy by beamlet propagators[C]. Salt Lake City: SEG Technical Program Expanded Abstracts: 1352-1355.

[21]
WU RUSHAN, CHEN LING, 2006. Directional illumination analysis using beamlet decomposition and propagation[J]. Geophysics, 71(4): S147-S159.

[22]
XIE XIAOBI, JIN SHENGWEN, WU RUSHAN, 2006. Wave-equation-based seismic illumination analysis[J]. Geophysics, 71(5): S169-S177.

[23]
XIE XIAOBI, YANG HUI, 2008. A full-wave equation based seismic illumination analysis method[C]. Rome: 70th conference & Exhibition, European Association of Geoscientists & Engineers, Extended Abstracts: 284.

[24]
YOON K, GUO MANHONG, CAI JUN, et al, 2011. 3D RTM angle gathers from source wave propagation direction and dip of reflector[C]. San Antonio: SEG Technical Program Expanded Abstracts: 3136-3140.

[25]
YOON K, MARFURT K J, 2006. Reverse-time migration using the Poynting vector[J]. Exploration Geophysics, 37(1): 102-107.

Options
Outlines

/

〈 〉