Search
E-mail
RSS

Online submission Editor-in-chief Peer review Staff Login

Journal of Tropical Oceanography >

2017 , Vol. 36 >Issue 5: 1 - 8

DOI: https://doi.org/10.11978/2016131

Orginal Article

The development and application of river-tide harmonic model

  • OU Suying ,
  • YANG Qingshu ,
  • YANG Hao ,
  • HU Shuai
Expand
  • Institute of Estuarine and Coastal Research, Sun Yat-sen University, State and Local Joint Engineering Laboratory of Estuarine Hydraulic Technology, Guangzhou 510275, China

Author:OU Suying.E-mail:

Received date: 2016-12-14

  Request revised date: 2017-02-22

  Online published: 2017-09-22

Supported by

National Key Research and Development Program of China (2016YFC0402600); National Natural Science Foundation of China (41106015)

Copyright

热带海洋学报编辑部
Fold

Abstract

With the modulation of river flows, tides in delta and estuary are generally nonstationary and nonlinear, which is difficult for analysis and prediction. Combined the interaction of river and tide in an estuary with the concept of traditional Harmonic Analysis (HA), the River-Tidal Harmonic Analysis (RTHA) model was built, and the non-stationary tide in the Pearl River delta under daily Pearl River discharge was analyzed and predicted by the model. The results show that the RTHA model performed well when analyzing and predicting the hourly tidal water level and high-low tide on annual scale, which gave root-mean-square error of 0.12~0.17 m, and correlation coefficients of 91%~98%. Especially in the upper and middle channels of the delta where river dynamics are dominant, the results of the RTHA model are far better than those of the HA model. The results of the RTHA model show that the amplitudes of diurnal (K1), semidiurnal and third-diurnal constituents decrease rapidly in flood season with large river discharge and increase in dry season, but the amplitudes of quarter-diurnal constituents at Hengmen station increase in flood season and decrease in dry season. When the Pearl River discharge increases, the constituents’ phase increases and the wave celerity decreases in flood season, while the damping ratio of tidal amplitudes was about 10%~30% in the dry season and increased to 70%~80% in the flood season.

Key words： tide; river discharge; river-tide interaction; river-tidal harmonic analysis model; estuary; delta

Cite this article

OU Suying , YANG Qingshu , YANG Hao , HU Shuai . The development and application of river-tide harmonic model[J]. Journal of Tropical Oceanography, 2017 , 36(5) : 1 -8 . DOI: 10.11978/2016131

河口三角洲地区是典型的河流动力和海洋动力交互控制地带, 同时又是多尺度动力结构的耦合区。径流和潮汐是不同尺度的两种动力结构, 径潮相互作用表现为径流的不确定性变化影响控制河口潮汐的时空变化, 使河口潮汐特别是径流优势型河口段具有与外海天文潮汐明显不同的非线性变化及气候态变化特征(Godin, 1985; Matte et al, 2013)。径流影响下河口三角洲潮汐的非确定性变化加剧了径潮动力研究的困难, 导致水位预报的精度低、传统调和分析方法的误差大。
为提高河口三角洲地区非线性潮汐研究的精度, 研究者们采用多种方法分析河口三角洲潮汐变化及径流对潮汐的影响(Jay et al, 1997; Lee, 2004; 欧素英 等, 2004, 2008; Sassi et al, 2013), 其中小波变换方法被广泛用于研究河口地区的不稳定潮汐信号。比如Jay等(1997)和欧素英等(2004)将河口三角洲不稳定的潮汐信号分离出全日分潮、半日分潮、四分之一分潮族的波动信号, 研究径流对不同分潮族的衰减效应及变化。Kukulka等(2003) 采用连续小波变换将哥伦比亚河感潮河段的水位分离出6组分潮波信号及亚潮信号, 计算日平均潮差, 结合一维线性圣维南方程的理论解, 分析径流影响下潮波振幅的衰减及日平均潮差的变化。但连续小波变换的频率分辨率低, 并不能分离出M2、K1、O1等确定频率的分潮波信息。为精确地分析径流占优河口段主要分潮的变化特征, Guo等(2015)避开径流量洪枯季变化所引起的误差, 采用分时段潮汐调和分析方法和连续小波变换结合, 对长江河口及其感潮河段的径潮相互作用进行研究。Matte等(2014)不仅考虑径流, 同时还考虑外海潮汐边界包括潮水位、亚潮水位的驱动影响, 认为河口段任意位置的分潮振幅和位相都受到外海潮汐和上游径流的非线性影响, 在传统调和分析方法的基础上, 建立上游径流和外海潮汐驱动的不稳定潮汐调和分析模型(NS_tide), 并利用该方法研究了圣劳伦斯河口潮水位不同时间尺度的变化特别是洪、枯季变化。
本文针对径潮耦合的非线性问题, 采用Matte等(2013)非线性调和分析思路, 但不考虑外海潮汐边界的驱动影响, 而认为河口任意位置的潮汐振幅和位相的变化主要受到上游径流量和地形变化的非线性调制影响, 如径流量增大, 全日分潮和半日分潮的振幅以不同幅度衰减, 三角洲河道地形下切, 水深加深, 水位下降, 引起分潮振幅不同程度的增加(Cai et al, 2012); 在此基础上, 假定分析和预报时间段河口水下地形不变, 建立径流影响下的潮汐调和分析和预报模型(river-tidal harmonic analysis, 简写RTHA)。以珠江三角洲典型河道为例, 对不同径流影响下的潮汐变化进行分析和预报; 并将RTHA模型用于研究珠江三角洲不同径流作用下典型水道低频潮汐波动、主要分潮振幅和位相的变化。

1 基于径潮耦合的调和分析方法

无径流影响时, 潮水位的变化可分解成多个分潮波(包括天文分潮、浅水分潮及气象分潮)余弦曲线的线性叠加:
其中z0为分析时间段的平均水位, z(tj)为tj时刻的水位, Hi、φi、σi为第i个分潮的调和常数(振幅、迟角)及圆频率, fi、gi为天文校正因子。经典的潮调和分析(简写HA)对式(1)的余弦函数分解为式(2), 其中,bi、ci为待定系数; 在式(2)基础上,根据逐时潮位或高低潮序列长度, 选择所有分潮或多个主要分潮, 采用最小二乘法求解各分潮的调和常数并以此预报任意时刻的潮水位。
对于不确定性的河口三角洲潮汐, 在多种非线性因素特别径流影响下, 式(1)中的调和常数随时间变化明显, 如径流量大, 分潮振幅随之减少, 潮波沿程衰减更快, 潮波变形更为明显。Kukulka等(2003)基于一维线性圣维南方程推导得出, 河口三角洲内潮波沿程衰减, 任一位置x的潮振幅
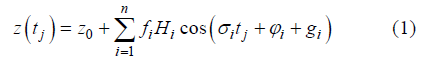
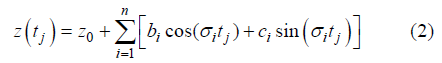
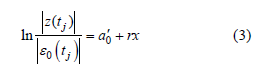
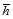式中r为衰减系数, ε0(tj)为河口口门位置x=0处的潮汐振幅, a0ʹ为综合常参数。衰减系数r为波速、水深、径流量及河道摩擦系数的函数(Cai et al, 2012; Matte et al, 2013)。若摩擦系数采用曼宁公式, 摩擦系数与波速c0均为水深的函数, 则衰减系数r可简写为水深 、径流量Q(tj)的函数,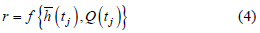
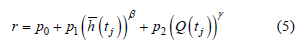
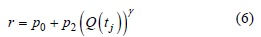
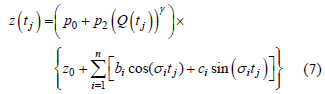
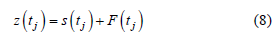
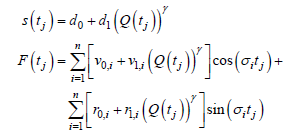
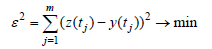
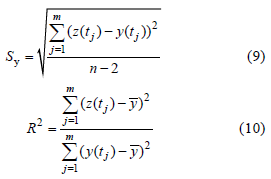
根据Kukulka等(2003)和Matte等(2013), 将衰减系数r约以多项式形式表述如下:
式中p0、p1、p2及β、γ均为待定常数。与Matte等(2013)不同的是, 式(4)并不考虑外海边界潮汐的驱动。假定河道平均水深为常数, 不随时间发生变化, 则式(5)中平均水深项可归并到待定常数p0, 式(5)简写为
也即是说, 河口潮汐随时间的非线性衰减变化仅受控于径流的变化。
结合式(1)、(3)和(6), 径流影响下任意位置x潮水位的变化为
据研究(Jay et al, 1997; Guo et al, 2015), 径流对不同分潮的影响程度不同, 径流影响下半日分潮的衰减大于全日分潮。将径流对每一个分潮的调制影响都采用不同的待定参数, 式(7)可写成
其中,
式中 d0、d1为状态模型的待定参数, v0、v1和 r0、r1为待定参数, γ为待定幂指数, 如Matte等(2013)通过迭代确定。式(8)即为径流影响下的RTHA模型, s(tj)为河底高程或水深变化、海平面、流量等引起的平均水面(MSL)变化, 随径流量、海平面的改变而改变, 称为平均水面状态模型。F(tj)描述不同径流条件对分潮的调制影响及亚潮水位的影响。
设河口三角洲任意位置、采用时间间隔为Δt的观测潮位为y(tj) (j=1, …, m), 根据资料的长度mΔt、分潮的频率差和Rayleigh判据Δσ=max((mΔt)-1, σi-σj), 选择要进行调和分析的分潮。将tj、σi、Q(tj)代入式(8), 要求模型结果z(tj)与实测水位y(tj)的误差平方和最小, 即
基于MATLAB平台的潮汐调和分析软件(T_tide)(Pawlowicz et al, 2002), 选择对应资料长度的分潮, 包括全日分潮、半日分潮和高频分潮, 对实测潮水位进行回归拟合, 潮调和回归模型效果以标准误差估计Sy和相关指数R2表示:

2 基于RTHA的珠江三角洲径潮相互作用分析

珠江作为国内第二大河流, 每年携带306×109m3的淡水径流进入珠江河口区, 径流对河口区潮汐动力的影响极为明显。同时, 因为珠江是一个由东江、西江、北江及诸小河构成的复合水系, 由西江汇入河口区的流量占珠江流量的70%, 且珠江三角洲网河区河汊发育, 水网密布, 多汊分流, 八口入海 (图1), 因此, 珠江河口不同汊道所受径流影响强弱有所差异。
本文首先选取主要由西江入海径流控制、径流影响显著的磨刀门水道灯笼山站、小榄水道及横门水道的小榄、马鞍、横门站的逐时水位序列, 同时选取整个三角洲包括径优型和潮优型水道多个站位的高、低潮位序列(站位见图1), 分别利用马口站或西江高要站、北江石角站、东江博罗站的对应时间段的日平均流量进行驱动, 采用基于径潮耦合的调和分析方法(RTHA), 对两类年尺度的潮水位数据进行径潮信号分离, 研究三角洲网河的径潮相互作用。

2.1 RTHA模型的效果评价

珠江河口三角洲地区是典型的多尺度动力结构的耦合区。珠江径流表现出明显的季节尺度和年际尺度, 影响河口区潮汐的短期和长期变化。径流大的洪季和丰水年份, 珠江径流对河口区潮汐的非线性作用越显著。
本文首先以典型丰水年(1994年、1998年)横门水道的横门站、小榄站、马鞍站及磨刀门水道的灯笼山站(站位见图1)逐时水位序列为例, 分别利用传统调和分析方法(HA)和RTHA(公式8、9、10), 分析囊括径流的季节尺度在内的1994年逐时水位序列。由于横门水道和磨刀门水道仅受到西江马口站入海流量的驱动(图1), 因此RTHA以西江马口站日平均径流量为驱动条件(图2a), 分析结果见表1和图2b。比较传统调和方法(HA)和RTHA方法的计算标准误差和相关指数(表1), 从中可以看出, RTHA模型的精度明显高于HA模型, HA模型的分析结果仅为原来水位信号的4%~68%, 水位信号的分离效果差, 而口门位置(灯笼山、横门)的RTHA标准误差估计约0.12m, RTHA模型后报值(计算值)与实测数据的吻合度高, 两者相关指数达到94.5%。径流影响越显著的三角洲中上部地区, 如小榄站和马鞍站, HA偏差越大, 方差贡献率越少, 一般小于10%, 而RTHA模型的方差贡献率达到或超过96%, 可以很好地模拟径流和潮汐共同作用下的逐时水位变化过程, 有效进行径潮水位信号的剥离。如图2b所示, 洪季径流强, 潮汐作用弱, 潮差小, 河道及口门位置水位受径流控制显著抬高, RTHA的模拟比HA分析结果更吻合三角洲径流影响下的水位过程; 枯水季节径流弱, 潮差大, HA和RTHA的结果都非常接近。
Fig. 1 The Pearl River delta and observation stations

图1 珠江三角洲网河体系及站位图

Tab.1 The analyzed and predicted results of RTHA and HA models based on hourly tidal water level

表1 逐时水位序列的HA、RTHA分析和预报效果

站位 资料时间 RTHA模型 HA模型
径流 流量指数γ 分潮个数 Sy/m R2/% Sy/m R2/%
灯笼山 分析时间段
1994-01至1994-12		 马口日平均径流 1.15 27 0.12 94.2 0.27 60.9
横门 0.12 94.5 0.18 64.3
马鞍 0.16 95.9 0.78 10.5
小榄 0.22 96.4 1.11 4.1
灯笼山 预报时间段
1998-01至1998-12		 马口日平均径流 1.15 27 0.20 94.7 0.26 67.5
横门 0.17 91.5 0.24 61.3
马鞍 0.19 95.4 0.54 43.8
小榄 0.24 99.4 0.76 37.0
其次, 本文选取三角洲河优型及潮优型水道中不同空间位置共17个站位的1987—1990年高低潮时间序列进行模型检验, 站位见图1。由于西江和北江的入海径流量同时影响西北江三角洲的潮汐, 因此采用西江高要站和北江石角站的日平均流量和作为西北江三角洲RTHA模型的驱动流量, 东江三角洲采用东江博罗站的日平均流量进行驱动, 利用RTHA模型进行水位信号分离、重构, 各站计算值和实测值的标准误差估计与相关指数见表2。RTHA模型分析后报1987—1990年的高低潮位序列的标准误差为0.14~0.22m, 小于HA模型的标准误差0.18~1.28m; RTHA模型的分析精度超过91%, 而HA模型的分析精度最低低至30%。潮优型虎门水道东侧的大盛、泗盛围及崖门水道的官冲站, HA和RTHA的分析精度接近, 相关指数都超过0.92, 径流对潮优型口门水道潮汐的调制影响作用弱; 径优型口门水道如横门水道横门站、磨刀门水道灯笼山站, RTHA模型的精度高于HA模型, 径流对潮汐的变化有一定的影响, 特别是大洪水过程, 径流的影响极为明显。越往三角洲中上部, 径流对河道潮汐的影响越显著, HA的分析误差极大, 而考虑径流调制影响的RTHA模型的分析精度高, 小榄、三多、南华、马口等站相关指数为0.93~0.98, 也即是说, 该回归模型可以更好地分离、重构三角洲高低潮水位时间序列中的径潮信号, 以用于三角洲地区的径潮相互作用过程的研究。
Fig. 2 The water level deviations of HA and RTHA models at Xiaolan (b) under the Makou daily river flow (a) during 1994

图2 1994年马口日平均流量(a)驱动下小榄逐时水位序列HA与RTHA的结果(b)

Tab.2 Comparison between analyzed and predicted results of RTHA and HA models based on high and low tidal water level data

表2 高低潮水位序列的HA、RTHA分析和预报效果

站位 分析时间段: 1987—1989 预报时间段: 1990年1—12月
RTHA模型 HA模型 RTHA模型 HA模型
Sy/m R2/% Sy/m R2/% Sy/m R2/% Sy/m R2/%
大盛 0.17 96.5 0.19 95.7 0.19 95.5 0.21 94.3
泗盛围 0.17 96.2 0.19 95.1 0.19 95.5 0.21 94.3
横门 0.17 92.9 0.20 90.5 0.19 93.1 0.19 92.9
板沙尾 0.15 94.6 0.27 82.6 0.19 92.5 0.28 81.7
马鞍 0.16 92.7 0.31 71.5 0.17 92.7 0.30 74.9
小榄 0.15 94.3 0.44 52.4 0.21 90.1 0.44 51.7
南华 0.16 96.0 0.62 37.2 空白 空白 空白 空白
容奇 0.16 93.3 0.35 69.4 0.19 92.4 0.33 72.0
三多 0.18 94.4 0.58 43.4 0.27 90.3 0.57 44.1
三善滘 0.16 93.1 0.29 78.6 0.25 90.1 0.29 76.6
马口 0.22 98.0 1.28 30.5 空白 空白 空白 空白
甘竹 0.17 95.9 0.71 31.2 0.25 91.7 0.72 39.3
江门 0.16 93.2 0.47 42.3 0.21 91.1 0.46 41.0
竹银 0.15 91.2 0.24 76.1 0.17 90.6 0.25 75.7
灯笼山 0.16 91.8 0.18 88.7 0.20 90.8 0.21 90.2
黄金 0.17 93.2 0.19 92.2 0.17 91.9 0.17 91.7
官冲 0.20 92.6 0.21 92.0 空白 空白 空白 空白

注: 预报时段部分站位缺失数据。

基于各站潮水位序列的RTHA分析, 也可进行径流驱动下三角洲潮水位的预报, 其预报精度明显高于HA方法。以灯笼山、横门等四站1994年的RTHA分析为基础, 利用马口站1998年的日平均流量驱动, 预报1998年横门、灯笼山等站的逐时潮水位变化, HA和RTHA的预报及统计结果也见表1。从表1中可以看出, RTHA的预报值与实测值的相关指数高于90%, 预报结果显著优于HA的结果(37%~68%)。同时, 以1987—1989年的高低潮水位的RTHA分析结果, 对1990年全年的高低潮时刻的潮水位进行预报, 预报结果与实测结果的标准误差及相关指数见表2。结果显示, RTHA模型预报值与实测高低潮位的相关指数都大于0.9。与传统HA相比, RTHA模型的预报精度越往三角洲中上段, 其精度越高。

2.2 珠江三角洲径潮相互作用机理分析

RTHA模型可以很好地模拟径流影响下的潮汐, 分离各站的径、潮信号, 有效反映出河口三角洲地区径潮作用过程。由式(8)建立各分潮振幅、位相与流量的关系:
以1994年横门水道及其上段鸡鸦水道、小榄水道的径潮作用为例, 利用式(11)计算径流影响下水位及各分潮的调和常数变化, 如横门及马鞍的M2分潮振幅随径流的增加而呈非线性(如二阶多项式)的衰减, 公式如下:
对3个站位的水位信号进行分离计算, 分离出径流影响下的河道水位s(tj), 同时计算周期大于7天的亚潮振幅(径潮耦合的低频波动, 包括半月周期、月周期的潮汐变化)、2个主要全日分潮及2个半日分潮的振幅、D3分潮族、D4分潮族的振幅变化, 结果如图3所示。
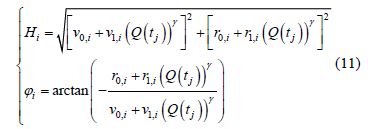
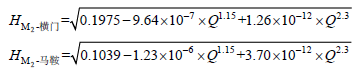
Fig. 3 Seasonal changes of river-tide by RTHA model at Hengmen, Maan and Xiaolan stations during 1994. a is mean river water level; b is low frequency amplitude with period greater than seven days; c is K1 amplitude; d is M2 amplitude; e and f are amplitudes of D3 and D4, respectively; g and h represent the phase of K1 and M2 constituents, respectively, with M2 phase exceeding 360°

图3 1994年横门、马鞍、小榄站RTHA分解的主要分潮及亚潮年内变化
a. 径流引起的余水位; b. 大于7天的低频波动; c. K1分潮振幅; d. M2分潮振幅; e. D3分潮族振幅; f. D4分潮族振幅; g. K1分潮位相; h. M2分潮位相, 其中M2分潮的位相未曾减去360º

马口1994年径流量的变化如图2a所示, 夏季6—8月马口入海流量迅速增大。在马口流量的年内变化尺度的影响下, 横门等站的潮汐随之发生相应尺度的变化(图3)。由图3可知, 随着径流的增大, 夏季各站径流引起的余水位显著增大(图3a), 周期大于7天的低频波动的振幅随径流的增大而增大(图3b), 径流的年内尺度变化加强了潮汐的低频波动幅度。但径流对全日分潮和半日分潮的调制与潮汐低频波动有明显差异, 径流量小的枯水季节, 全日分潮K1、O1及半日分潮M2、S2的振幅大, 径流量大的洪水季节, 各站全日分潮振幅和半日分潮振幅迅速减小(图3c、d)。径流影响下浅水分潮振幅变化更为复杂, 浅水分潮以枯水季节振幅较大且变化较小, 随着流量增大, D3分潮族振幅减小(图3e), 但口门段(横门站)D4分潮族振幅随流量增大而增大, 夏季达到最大, 而三角洲中段的小榄站D4分潮族振幅随流量增大而减小(图3f)。
径流量的不同尺度变化对河口潮波传播过程的调制同样明显。从伶仃洋传入横门水道的潮波, 向上游方向沿不同汊道传播到马鞍、小榄, 潮波振幅受地形、径流的影响沿程衰减。以马鞍或小榄站各分潮波振幅与横门站的潮波振幅之比rd来考察径流年内尺度变化对潮波传播的影响, 如图4所示, 各分潮振幅的比值都随径流量的季节性增大而减少, 夏季6—8月最小。随着径流量的显著增大, 水面梯度增加(径流引起的水面梯度及低频波动引起的水面梯度, 图3a、b), 潮波向上游传播过程中为克服反向压力梯度所消耗的能量越大, 潮波振幅沿程衰减得愈快, 从枯季到洪水季节, 自横门到马鞍、小榄, M2、K1分潮衰减幅度由20%~30%增加到70%~80%(图4a、b), D3、D4分潮族振幅衰减幅度由枯季的10%左右增加到70%(图4c、d); 同时, 分潮的传播速度随径流量的增大而明显降低, 如图3g、h所示, 夏季M2、K1分潮迟角明显增加, 同样自横门传播到小榄或马鞍, 全日分潮和半日分潮所需时间都显著增加。
Fig. 4 Seasonal variation of damping ratio of M2, , K1, D3 and D4 constituents along Hengmen Channel under Makou daily river flow during 1994. a, b, c, and d are the damping ratios of M2, K1, D3 and D4 respectively

图4 1994年马口径流影响下马鞍、小榄的K1(a)、M2(b)、D3(c)、D4(d)分潮振幅相对于横门站分潮振幅之比值的年内变化

3 结论

受径流、地形等因素的影响, 感潮河道、河口三角洲的潮汐非线性效应显著, 潮汐的时间变化复杂, 径流对潮汐的影响、非线性潮汐的分析和预报一直是众多研究者关注的焦点。本文基于三角洲河道内径潮相互作用研究及传统潮汐调和分析的理论基础, 建 立径潮耦合的调和分析模型(RTHA模型), 用于分析和预报河口三角洲地区的非恒定潮汐变化; 以珠江三角洲为研究对象, 采用RTHA模型对径流年内变化显著的1994年、1998年逐时潮位及1987—1990年高低潮水位进行分析, 分离、重构三角洲各站的径潮信号。结果显示, 对于河口年尺度或多年尺度的潮水位数据, RTHA模型分析和预报的标准误差为0.12~0.17m, 方差贡献(相关指数)为91%~98%, 优于经典潮汐调和分析(HA)结果; 特别是在径流作用强的河口三角洲中上段, RTHA模型精度远高于HA方法, 即径潮耦合的调和分析方法, 可以有效剥离径潮信号, 分析径潮相互作用, 亦可快速预报径优型河口的非线性潮汐。
基于RTHA的径潮信号分离, 研究珠江三角洲典型径优型水道的径潮相互作用过程, 结果表明,珠江径流量的年内尺度变化(洪枯季变化)加强了潮汐低频波动的年内变化幅度, 导致全日分潮、半日分潮、三分之一分潮的振幅洪季小、枯季大, 口门段四分之一分潮的振幅洪季大、枯季小; 珠江径流量的洪枯季变化引起潮汐沿程传播的季节变化, 洪季全日分潮、半日分潮传播速度变小(位相增大), 分潮振幅沿程衰减幅度显著增大, 自枯季的10%~30%迅速增加到洪季的70%~80%。

The authors have declared that no competing interests exist.

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
欧素英, 杨清书, 2004. 珠江三角洲网河区径流潮流相互作用分析[J]. 海洋学报, 26(1): 125-131.

OU SUYING, YANG QINGSHU, 2004. Interaction of fluctuating river flow with a barotropic tide in river network of the Zhujiang Delta[J]. Acta Oceanologica Sinica, 26(1): 125-131 (in Chinese).

[2]
欧素英, 杨清书, 2008. 人工神经网络模型在航道、港口潮水位预报中的应用[J]. 水利水运工程学报, (2): 67-70.

OU SUYING, YANG QINGSHU, 2008. Back-propagation artificial neural network model for prediction of tidal water level[J]. Hydro-Science and Engineering, (2): 67-70 (in Chinese).

[3]
CAI HUAYANG, SAVENIJE H H G, YANG QINGSHU, et al, 2012. Influence of river discharge and dredging on tidal wave propagation: Modaomen Estuary case[J]. Journal of Hydraulic Engineering, 138(10): 885-896.

[4]
GODIN G, 1985. Modification of river tides by the discharge[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 111(2): 257-274.

[5]
GUO LEICEHNG, VAN DER WEGEN M, JAY D A, et al, 2015. River-tide dynamics: exploration of nonstationary and nonlinear tidal behavior in the Yangtze River estuary[J]. Journal of Geophysical Research, 120(5): 3499-3521, doi: 10.1002/2014JC010491.

[6]
JAY D A, FLINCHEM E P, 1997. Interaction of fluctuating river flow with a barotropic tide: A demonstration of wavelet tidal analysis methods[J]. Journal of Geophysical Research, 102(C3): 5705-5720.

[7]
KUKULKA T, JAY D A, 2003. Impacts of Columbia River discharge on salmonid habitat: 1. A nonstationary fluvial tide model[J]. Journal of Geophysical Research, 108(C9): 3293, doi: 10.1029/2002JC001382.

[8]
LEE T L, 2004. Back-propagation neural network for long-term tidal predictions[J]. Ocean Engineering, 31(2): 225-238.

[9]
MATTE P, JAY D A, ZARON E D, 2013. Adaptation of classical tidal harmonic analysis to nonstationary tides, with application to river tides[J]. Journal of Atmospheric and Oceanic Technology, 30(3): 569-589.

[10]
MATTE P, SECRETAN Y, MORIN J, 2014. Temporal and spatial variability of tidal-fluvial dynamics in the St. Lawrence fluvial estuary: an application of nonstationary tidal harmonic analysis[J]. Journal of Geophysical Research, 119(9): 5724-5744, doi: 10.1002/2014JC009791.

[11]
PAWLOWICZ R, BEARDSLEY B, LENTZ S, 2002. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE[J]. Computers & Geosciences, 28(8): 929-937.

[12]
SASSI M G, HOITINK A J F, 2013. River flow controls on tides and tide-mean water level profiles in a tidal freshwater river[J]. Journal of Geophysical Research, 118(9): 4139-4151, doi: 10.1002/jgrc.20297.

Options
Outlines

/

〈 〉